题目内容
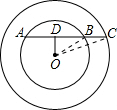
如图所示，以O为圆心的两个同心圆中，小圆的弦AB的延长线交大圆于C，若AB=3，BC=1，则与圆环的面积最接近的整数是（ ）
| A．9 | B．10 | C．15 | D．13 |
连接OB，OC，
根据垂径定理，得BD=1.5，则CD=2.5，
∵OB2=OD2+BD2，OC2=OD2+CD2，
根据勾股定理结合圆环面积公式得：
圆环的面积=π•OC2-π•OB2=π•（OC2-OB2）=π•（CD2-DB2）=π•（2.52-1.52）=π•（6.25-2.25）=4π≈12.56．
故选D．
根据垂径定理，得BD=1.5，则CD=2.5，
∵OB2=OD2+BD2，OC2=OD2+CD2，
根据勾股定理结合圆环面积公式得：
圆环的面积=π•OC2-π•OB2=π•（OC2-OB2）=π•（CD2-DB2）=π•（2.52-1.52）=π•（6.25-2.25）=4π≈12.56．
故选D．
练习册系列答案
作业辅导系列答案
相关题目
、B（8，0）两点，圆心C在第四象限．
