题目内容
【题目】已知直线![]() (其中
(其中![]() 为常数,
为常数,![]() ),
),![]() 取不同数值时,可得不同直线,请研究这些直线的共同特征.
取不同数值时,可得不同直线,请研究这些直线的共同特征.
实践操作
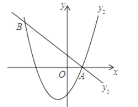
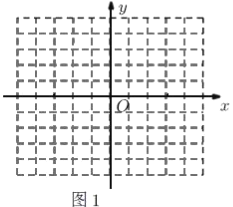
(1)当![]() 时,直线
时,直线![]() 的解析式为________,请在图1中画出图象.
的解析式为________,请在图1中画出图象.
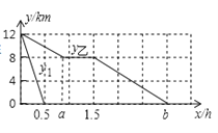
当![]() 时,直线
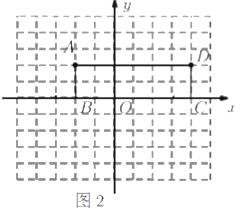
时,直线![]() 的解析式为________,请在图2中画出图象
的解析式为________,请在图2中画出图象
(2)探索发现:
直线![]() 必经过点(_______,_______).
必经过点(_______,_______).
(3)类比迁移:
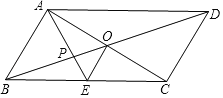
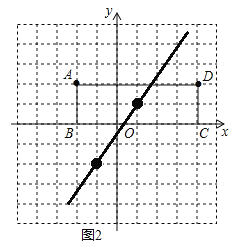
矩形![]() 如图2所示,若直线
如图2所示,若直线![]() 分矩形
分矩形![]() 的面积为相等的两部分,请在图中直接画出这条直线.
的面积为相等的两部分,请在图中直接画出这条直线.
【答案】(1)![]() :
:![]() ;
;![]() :
:![]() ;(2)
;(2)![]() ,
,![]() ;(3)画图见解析.
;(3)画图见解析.
【解析】
(1)把当k=1,k=2时,分别代入求一次函数的解析式即可, (2)把![]() 转化为
转化为![]() ,可得无论k取何值(0除外),直线
,可得无论k取何值(0除外),直线![]() 必经过定点可得答案; (3)先把直线
必经过定点可得答案; (3)先把直线![]() 转化为
转化为![]() ,得到直线
,得到直线![]() 无论k取何值,总过定点,再根据过矩形对角线的交点的直线把矩形的面积平分,即可画出直线.
无论k取何值,总过定点,再根据过矩形对角线的交点的直线把矩形的面积平分,即可画出直线.
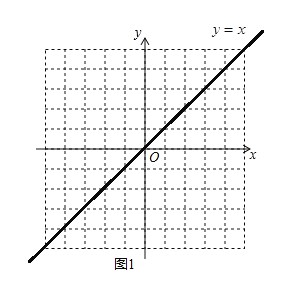
解:(1)当![]() 时,直线
时,直线![]() 的解析式为:
的解析式为:![]() ,如图1.
,如图1.
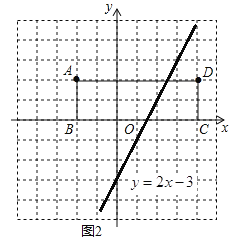
当![]() 时,直线
时,直线![]() 的解析式为
的解析式为![]() .如图2,
.如图2,
(2)![]() ,
,
![]()
![]() 无论
无论![]() 取值(
取值(![]() 除外).
除外).
直线![]() 必经过点
必经过点![]() .
.
(3)![]() 直线
直线![]()
![]()
![]() 无论
无论![]() 取何值.总过点
取何值.总过点![]()
因为矩形是中心对称图形,对称中心为对角线的交点,过矩形对角线的交点的直线平分矩形的面积,所以找出对角线的交点![]() ,通过两点的直线平分矩形
,通过两点的直线平分矩形![]() 的面积.作出图形如图2.
的面积.作出图形如图2.

练习册系列答案
相关题目
【题目】某经销商从市场得知如下信息:
A 品牌手表 | B 品牌手表 | |
进价(元/块) | 700 | 100 |
售价(元/块) | 900 | 160 |
他计划用 40000 元资金一次性购进这两种品牌手表共 100 块,设该经销商购进 A 品牌手表 x 块,这两种品牌手表全部销售完后获得利润为 y 元.
(1)试写出 y 与 x 之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于 12650 元,该经销商有哪几种进货方案;
(3)选择哪种进货方案,该经销商可获利最大;最大利润是多少元.