题目内容
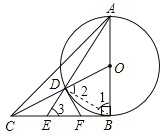
【题目】已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④![]() .其中正确的只有____________________.(填序号)
.其中正确的只有____________________.(填序号)

【答案】①、②、④
【解析】试题分析:先连接BD,利用相似三角形的判定以及切线的性质定理得出DF=FB,进而分别得出△CDE∽△CBD以及△CDF∽△CBO,再根据相似三角形的性质分别分析即可得出答案.
①连接BD,∵AB为直径,∴∠ADB=90°,∴∠DBE+∠3=90°,∵∠ABC=90°,
∴∠1+∠DBE=90°,∴∠1=∠3,又∵DO=BO,∴∠1=∠2,∴∠2=∠3,
∴∠CDB=∠CED,∵∠DCB=∠ECD,∴△CDE∽△CBD,∴![]() ,故①正确;
,故①正确;
②∵过D作⊙O的切线交BC于点F,∴FD是⊙O的切线,∵∠ABC=90°,
∴CB是⊙O的切线,∴FB=DF,∴∠FDB=∠FBD,∴∠1=∠FDE,∴∠FDE=∠3,
∴DF=EF,∴EF=FB,∴EB=2EF,∵在Rt△ABE中,BD⊥AE,∴![]() ,
,
∴![]() ,故②正确;
,故②正确;
③∵AO=DO,∴∠OAD=∠ADO,假设③∠OCB=∠EAB成立,则∠OCB=0.5∠COB,
∴∠OCB=30°,而![]() ,与tan30°=
,与tan30°= ![]() 矛盾,
矛盾,
故③∠OCB=∠EAB不成立,故此选项错误;
④∵∠CDF=∠CBO=90°,∠DCF=∠OCB,∴△CDF∽△CBO,∴![]() ,∴
,∴![]() ,
,
∵AB=BC,∴DF=0.5CD;故④正确.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲队的平均成绩和方差;
(3)已知乙队成绩的方差是1 ![]() ,则成绩较为整齐的是哪一队.
,则成绩较为整齐的是哪一队.
