题目内容
【题目】如图,若点M是y轴正半轴上的任意一点,过点M作PQ∥x轴,分别交函数y=![]() (y>0)和y=
(y>0)和y=![]() (y>0)的图象于点P和Q,连接OP和OQ,则下列结论正确是( )
(y>0)的图象于点P和Q,连接OP和OQ,则下列结论正确是( )
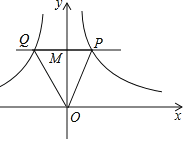
A.∠POQ不可能等于90°
B.![]()
C.这两个函数的图象一定关于y轴对称
D.△POQ的面积是![]()
【答案】D
【解析】
利用特例对A进行判断;根据反比例函数的几何意义得到S△OMQ=![]() OMQM=﹣
OMQM=﹣![]() k1,S△OMP=
k1,S△OMP=![]() OMPM=
OMPM=![]() k2,则可对B、D进行判断;利用关于y轴对称的点的坐标特征对C进行判断.
k2,则可对B、D进行判断;利用关于y轴对称的点的坐标特征对C进行判断.
解:A、当k1=3![]() ,k2=﹣
,k2=﹣![]() ,若Q(﹣1,
,若Q(﹣1,![]() ),P(3,
),P(3,![]() ),则∠POQ=90°,所以A选项错误;
),则∠POQ=90°,所以A选项错误;
B、因为PQ∥x轴,则S△OMQ=![]() OMQM=﹣
OMQM=﹣![]() k1,S△OMP=
k1,S△OMP=![]() OMPM=
OMPM=![]() k2,则
k2,则![]() =﹣
=﹣![]() ,所以B选项错误;
,所以B选项错误;
C、当k2=﹣k1时,这两个函数的图象一定关于y轴对称,所以C选项错误;
D、S△POQ=S△OMQ+S△OMP=![]() |k1|+
|k1|+![]() |k2|,所以D选项正确.
|k2|,所以D选项正确.
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 2 | … |
y | … | ﹣3 | ﹣4 | ﹣3 | 5 | … |
(1)求二次函数的表达式,并写出这个二次函数图象的顶点坐标;
(2)求出该函数图象与x轴的交点坐标.