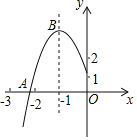题目内容
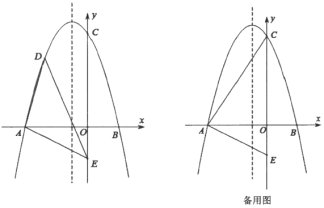
【题目】二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为-8、2,求二次函数的解析式
【答案】![]() 或
或![]()
【解析】
根据一元二次方程ax2+bx+c=0的两根为-8、2可得抛物线与x轴交点坐标为(-8,0)、(2,0),然后分开口向上与开口向下两种情况分类讨论进一步求解即可,
∵二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,且一元二次方程ax2+bx+c=0的两根为-8、2,
∴当x=-8时,y=0;x=2时,y=0,
∵tan∠ABC=3,
∴OC=6,
当抛物线开口向上时,C点坐标为(0,-6),
∴![]() ……①
……①
![]() ……②
……②
结合①②可得:![]() ,
,![]() ,
,
∴二次函数解析式为:![]() ;
;
当抛物线开口向下时,C点坐标为(0,6),
∴![]() ……③
……③
![]() ……④
……④
结合③④可得:![]() ,
,![]() ,
,
∴二次函数解析式为:![]() ,
,
综上所述,抛物线解析式为:![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球,放回、搅匀,下表是活动进行中的一组统计数据,
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.230 | 0.231 | 0.300 | 0.260 | 0.254 |
袋中白球的个数约为______.