Question

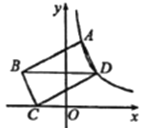
【题目】如图，CE是□ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E、连接AC，BE，DO，DO与AC交于点F，则下列结论：①四边形ACBE是菱形；②∠ACD＝∠BAE；③AF：BE＝2：3；④S四边形AFOE：S△COD＝2：3．其中正确的结论有（　　）个．

A. 1B. 2C. 3D. 4

Answer 1

【答案】C

【解析】

根据菱形的判定方法、平行线分线段成比例定理、直角三角形斜边中线的性质一一判断即可.

解：∵四边形ABCD是平行四边形，

∴AB∥CD，AB＝CD，

∵EC垂直平分AB，

∴OA＝OB＝AB＝DC，CD⊥CE，

∵OA∥DC，

∴＝＝＝，

∴AE＝AD，OE＝OC，

∵OA＝OB，OE＝OC，

∴四边形ACBE是平行四边形，

∵AB⊥EC，

∴四边形ACBE是菱形，故①正确，

∵∠DCE＝90°，DA＝AE，

∴AC＝AD＝AE，

∴∠ACD＝∠ADC＝∠BAE，故②正确，

∵OA∥CD，

∴＝＝，

∴＝＝，故③错误，

设△AOF的面积为a，则△OFC的面积为2a，△CDF的面积为4a，△AOC的面积＝△AOE的面积＝3a，

∴四边形AFOE的面积为4a，△ODC的面积为6a

∴S四边形AFOE：S△COD＝2：3．故④正确，

故选：C．