ƒøƒ⁄»ð
°æƒø°ø»ÁÕºÀ˘ 棨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨π˝µ„A£®©Å![]() £¨0£©µƒ¡ΩÃı÷±œþ∑÷±Ωªy÷·”⁄B°¢C¡Ωµ„£¨«“B°¢C¡Ωµ„µƒ◊ð◊¯±Í∑÷± «“ª‘™∂˛¥Œ∑Ω≥Ãx2©Å2x©Å3=0µƒ¡Ω∏ˆ∏˘
£¨0£©µƒ¡ΩÃı÷±œþ∑÷±Ωªy÷·”⁄B°¢C¡Ωµ„£¨«“B°¢C¡Ωµ„µƒ◊ð◊¯±Í∑÷± «“ª‘™∂˛¥Œ∑Ω≥Ãx2©Å2x©Å3=0µƒ¡Ω∏ˆ∏˘
£®1£©«Ûœþ∂ŒBCµƒ≥§∂»£ª
£®2£© ‘Œ £∫÷±œþAC”Î÷±œþAB «∑Ò¥π÷±£ø«ÎÀµ√˜¿Ì”…£ª
£®3£©»Ùµ„D‘⁄÷±œþAC…œ£¨«“DB=DC£¨«Ûµ„Dµƒ◊¯±Í£ª
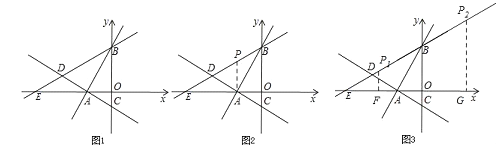
£®4£©‘⁄£®3£©µƒÃıº˛œ¬£¨÷±œþBD…œ «∑ҥʑ⁄µ„P£¨ π“‘A°¢B°¢P»˝µ„Œ™∂•µ„µƒ»˝Ω«–Œ «µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆPµ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ

°æ¥∞∏°ø£®1£©4£ª£®2£©AC°ÕAB£¨¿Ì”…º˚Ω‚Œˆ£ª£®3£©D£®©Å2![]() £¨1£©£ª£®4£©µ„Pµƒ◊¯±ÍŒ™£®©Å3
£¨1£©£ª£®4£©µ„Pµƒ◊¯±ÍŒ™£®©Å3![]() £¨0£©£¨£®©Å
£¨0£©£¨£®©Å![]() £¨2£©£¨£®©Å3£¨3©Å
£¨2£©£¨£®©Å3£¨3©Å![]() £©£¨£®3£¨3+
£©£¨£®3£¨3+![]() £©£Æ
£©£Æ
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©Ω‚≥ˆ∑Ω≥Ã∫Û£¨º¥ø…«Û≥ˆB°¢C¡Ωµ„µƒ◊¯±Í£¨º¥ø…«Û≥ˆBCµƒ≥§∂»£ª£®2£©”…A°¢B°¢C»˝µ„◊¯±Íø…÷™OA2=OCOB£¨À˘“‘ø…÷§√˜°˜AOC°◊°˜BOA£¨¿˚”√∂‘”¶Ω«œýµ»º¥ø…«Û≥ˆ°œCAB=90°„£ª£®3£©»ð“◊«Ûµ√÷±œþACµƒΩ‚Œˆ Ω£¨”…DB=DCø…÷™£¨µ„D‘⁄BCµƒ¥π÷±∆Ω∑÷œþ…œ£¨À˘“‘Dµƒ◊ð◊¯±ÍŒ™1£¨Ω´∆‰¥˙»Î÷±œþACµƒΩ‚Œˆ Ωº¥ø…«Û≥ˆDµƒ◊¯±Í£ª£®4£©A°¢B°¢P»˝µ„Œ™∂•µ„µƒ»˝Ω«–Œ «µ»—¸»˝Ω«–Œ£¨ø…∑÷Œ™“‘œ¬»˝÷÷«Èøˆ£∫¢ŸAB=AP£ª¢⁄AB=BP£ª¢€AP=BP£ª»ª∫Û∑÷±«Û≥ˆPµƒ◊¯±Íº¥ø…£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©°þx2©Å2x©Å3=0£¨
°ýx=3ªÚx=©Å1£¨
°ýB£®0£¨3£©£¨C£®0£¨©Å1£©£¨
°ýBC=4£ª
£®2£©°þA£®©Å![]() £¨0£©£¨B£®0£¨3£©£¨C£®0£¨©Å1£©£¨
£¨0£©£¨B£®0£¨3£©£¨C£®0£¨©Å1£©£¨
°ýOA=![]() £¨OB=3£¨OC=1£¨
£¨OB=3£¨OC=1£¨
°ýOA2=OBOC£¨
°þ°œAOC=°œBOA=90°„£¨
°ý°˜AOC°◊°˜BOA£¨
°ý°œCAO=°œABO£¨
°ý°œCAO+°œBAO=°œABO+°œBAO=90°„£¨
°ý°œBAC=90°„£¨
°ýAC°ÕAB£ª
£®3£©…Ë÷±œþACµƒΩ‚Œˆ ΩŒ™y=kx+b£¨
∞—A£®©Å![]() £¨0£©∫ÕC£®0£¨©Å1£©¥˙»Îy=kx+b£¨
£¨0£©∫ÕC£®0£¨©Å1£©¥˙»Îy=kx+b£¨
°ý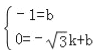 £¨
£¨
Ω‚µ√£∫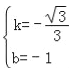 £¨
£¨
°ý÷±œþACµƒΩ‚Œˆ ΩŒ™£∫y=©Å![]() x©Å1£¨
x©Å1£¨
°þDB=DC£¨
°ýµ„D‘⁄œþ∂ŒBCµƒ¥π÷±∆Ω∑÷œþ…œ£¨
°ýDµƒ◊ð◊¯±ÍŒ™1£¨
°ý∞—y=1¥˙»Îy=©Å![]() x©Å1£¨
x©Å1£¨
°ýx=©Å2![]() £¨
£¨
°ýDµƒ◊¯±ÍŒ™£®©Å2![]() £¨1£©£¨
£¨1£©£¨
£®4£©…Ë÷±œþBDµƒΩ‚Œˆ ΩŒ™£∫y=mx+n£¨÷±œþBD”Îx÷·Ωª”⁄µ„E£¨
∞—B£®0£¨3£©∫ÕD£®©Å2![]() £¨1£©¥˙»Îy=mx+n£¨
£¨1£©¥˙»Îy=mx+n£¨
°ý![]() £¨
£¨
Ω‚µ√£¨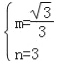
°ý÷±œþBDµƒΩ‚Œˆ ΩŒ™£∫y=![]() x+3£¨
x+3£¨
¡Óy=0¥˙»Îy=![]() x+3£¨
x+3£¨
°ýx=©Å3![]() £¨
£¨
°ýE£®©Å3![]() £¨0£©£¨
£¨0£©£¨
°ýOE=3![]() £¨
£¨
°ýtan°œBEC=![]() =
=![]() £¨
£¨
°ý°œBEO=30°„£¨
Õ¨¿Ìø…«Ûµ√£∫°œABO=30°„£¨
°ý°œABE=30°„£¨
µ±PA=AB ±£¨»ÁÕº1£¨
¥À ±£¨°œBEA=°œABE=30°„£¨
°ýEA=AB£¨
°ýP”ÎE÷ÿ∫œ£¨
°ýPµƒ◊¯±ÍŒ™£®©Å3![]() £¨0£©£¨
£¨0£©£¨
µ±PA=PB ±£¨»ÁÕº2£¨
¥À ±£¨°œPAB=°œPBA=30°„£¨
°þ°œABE=°œABO=30°„£¨
°ý°œPAB=°œABO£¨
°ýPA°ŒBC£¨
°ý°œPAO=90°„£¨
°ýµ„Pµƒ∫·◊¯±ÍŒ™©Å![]() £¨
£¨
¡Óx=©Å![]() ¥˙»Îy=
¥˙»Îy=![]() x+3£¨
x+3£¨
°ýy=2£¨
°ýP£®©Å![]() £¨2£©£¨
£¨2£©£¨
µ±PB=AB ±£¨»ÁÕº3£¨
°ý”…π¥π…∂®¿Ìø…«Ûµ√£∫AB=2![]() £¨EB=6£¨
£¨EB=6£¨
»Ùµ„P‘⁄y÷·◊Û≤ý ±£¨º«¥À ±µ„PŒ™P1£¨
π˝µ„P1◊˜P1F°Õx÷·”⁄µ„F£¨
°ýP1B=AB=2![]() £¨
£¨
°ýEP1=6©Å2![]() £¨
£¨
°ýsin°œBEO=![]() £¨
£¨
°ýFP1=3©Å![]() £¨
£¨
¡Óy=3©Å![]() ¥˙»Îy=
¥˙»Îy=![]() x+3£¨
x+3£¨
°ýx=©Å3£¨
°ýP1£®©Å3£¨3©Å![]() £©£¨
£©£¨
»Ùµ„P‘⁄y÷·µƒ”“≤ý ±£¨º«¥À ±µ„PŒ™P2£¨
π˝µ„P2◊˜P2G°Õx÷·”⁄µ„G£¨
°ýP2B=AB=2![]() £¨
£¨
°ýEP2=6+2![]() £¨
£¨
°ýsin°œBEO=![]() £¨
£¨
°ýGP2=3+![]() £¨
£¨
¡Óy=3+![]() ¥˙»Îy=
¥˙»Îy=![]() x+3£¨
x+3£¨
°ýx=3£¨
°ýP2£®3£¨3+![]() £©£¨
£©£¨
◊€…œÀ˘ ˆ£¨µ±A°¢B°¢P»˝µ„Œ™∂•µ„µƒ»˝Ω«–Œ «µ»—¸»˝Ω«–Œ ±£¨µ„Pµƒ◊¯±ÍŒ™£®©Å3![]() £¨0£©£¨£®©Å
£¨0£©£¨£®©Å![]() £¨2£©£¨£®©Å3£¨3©Å
£¨2£©£¨£®©Å3£¨3©Å![]() £©£¨£®3£¨3+
£©£¨£®3£¨3+![]() £©£Æ
£©£Æ

 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏°æƒø°øÔ˝øŒ…œ£¨∂‘∆þƒÍº∂1∞ýµƒƒ–…˙Ω¯––¡À100√◊≤‚ ‘£¨¥Ô±Í≥…º®Œ™15√Σ¨œ¬±Ì «ƒ≥–°◊È8√˚ƒ–…˙µƒ≥…º®≤‚ ‘º«¬º£¨∆‰÷–°∞+°∞±Ì æ≥…º®¥Û”⁄15√ΣÆ
-0.8 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
Œ £∫£®1£©’‚∏ˆ–°◊ȃ–…˙µƒ¥Ô±Í¬ Œ™∂ý…Ÿ£ø
£®2£©’‚∏ˆ–°◊ȃ–…˙µƒ∆Ωæ˘≥…º® «∂ý…Ÿ√Σø

