题目内容
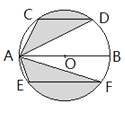
【题目】如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
解:因为,∠AOC:∠COD:∠BOD=2:3:4,
所以∠AOC= ,∠COD= ,∠BOD= ,
因为OE,OF分别平分∠AOC和∠BOD,
所以∠AOE= ,∠BOF= ,
所以∠EOF= ,
又因为 ,所以∠GOF=60°.

【答案】40°,60°,80°,20°,40°,120°,OG平分∠EOF
【解析】
根据互补两角的和为180°和角平分线的性质即可求得∠EOF的大小,即可解题.
∵∠AOC:∠COD:∠BOD=2:3:4,∠AOC+∠COD+∠BOD=180°,
∴∠AOC=40°,∠COD=60°,∠BOD=80°,
∵OE、OF分别平分∠AOC和∠BOD,
∴∠AOE=∠COE=20°,∠BOF=∠DOF=40°,
∴∠EOF=180°﹣20°﹣40°=120°,
∵OG平分∠EOF,
∴∠GOF=60°,
故答案为:40°,60°,80°,20°,40°,120°,OG平分∠EOF.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目