Question

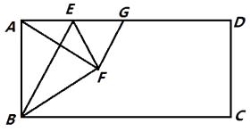
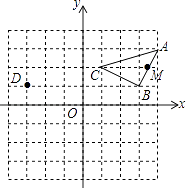
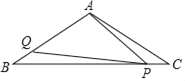
【题目】如图，已知△ABC中，AB=AC=cm，∠BAC=120°，点P在BC上从C向B运动，点Q在AB、AC上沿B→A→C运动，点P、Q分别从点C、B同时出发，速度均为1cm/s，当其中一点到达终点时两点同时停止运动，则当运动时间t=_____s时，△PAQ为直角三角形．

Answer 1

【答案】1或2或（6﹣9）．

【解析】

分三种情况：①∠AQP=90°,②∠APQ=90°,③∠PAQ=90°进行计算即可.

∵AB=AC=cm，∠BAC=120°，

∴∠B=∠C=30°,BC＝＝3，

有三种情况：

①当∠AQP=90°时,

有或,

即或

解得 或 ，

②当∠APQ=90°时,这种情况不成立；

③当∠PAQ=90°时，

有或,

即或，

解得或.

综上所述，当运动时间（单位：秒）为1或2或或时，△PAQ为直角三角形．

故答案为：1或2或或.