题目内容
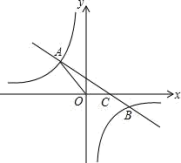
【题目】如图,抛物线W的图象与x轴交于A、O两点,顶点为点B(﹣1,﹣1).
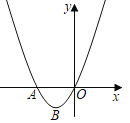
(1)求抛物线W的表达式;
(2)将抛物线W绕点A旋转180°得到抛物线V,使抛物线V的顶点为E,试通过计算判断抛物线V是否过点B;
(3)在抛物线W或V的图象上是否存在点D,使S△EBD=S△EBO?若存在,请求出点D的坐标.
【答案】(1)y=(x+1)2﹣1;(2)抛物线V是不经过点B;(3)在抛物线W或V的图象上存在点D,使S△EBD=S△EBO,D的坐标为(﹣3,3)或(﹣4,0)或(﹣1,﹣3).
【解析】
(1)把抛物线的解析式设成顶点式,代入原点坐标,便可求得解;
(2)根据对称性质求得E点坐标,再根据变化后的抛物线的形状和大小与原抛物线相同,开口方向相反,得新抛物线的解析式的二次项系数是原抛物线解析式的二次项系数的相反数,进而新抛物线的解析式,再验证是否经过B点便可;
(3)存在点D,过O点作BE的平行线,此平行线与抛物线W的另一交点便是D点,过(-4,0)作BE的平行线,此平行线与抛物线V的交点便是D点,求出这些交点的坐标便可.
(1)∵抛物线的顶点为B(﹣1,﹣1),
∴可设抛物线的解析式为y=a(x+1)2﹣1,
把O(0,0)代入,得0=a﹣1,
∴a=1,
∴抛物线的解析式为:y=(x+1)2﹣1;
(2)令y=0,有y=(x+1)2﹣1=0,
解得,x=0或﹣2,
∴A(﹣2,0),
∵将抛物线W绕点A旋转180°得到抛物线V,使抛物线V的顶点为E,B(﹣1,﹣1),
∴E(﹣3,1),
设抛物线V的解析式为:y=a'(x+3)2+1(a'≠0),
∵将抛物线W绕点A旋转180°得到抛物线V,抛物线W的解析式为:y=(x+1)2﹣1,
∴a'=﹣1,
∴抛物线V的解析式为:y=﹣(x+3)2+1,
当x=﹣1时,y=﹣4+1=﹣3≠﹣1,
∴抛物线V是不经过点B;
(3)设直线BE的解析式为:y=kx+b(k≠0),则
![]() ,
,
解得![]() ,
,
∴直线BE的解析式为:y=﹣x﹣2,
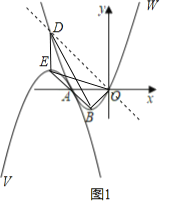
过O作OD//BE,与抛物线W交于D点,如图1,则S△OBE=S△DBE,
设OD的解析式为:y=﹣x+m,
把O(0,0)代入得,m=0,
∴OD的解析式为:y=﹣x,
联立方程组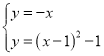 ,
,
解得![]() 或
或![]() ,
,
∴D(﹣3,3);
过抛物线V与x轴的交点F(﹣4,0)作FG//BE,与抛物线V交于另一点G,如图2,
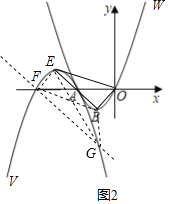
∵OA=AF=2,
∴S△OAE=S△AEF,S△OAB=S△ABF,
∴S△OBE=S△BEF=S△BEG,
设直线FG的解析式为:y=﹣x+n,
把F(﹣4,0)代入得n=﹣4,
∴直线FG的解析式为:y=﹣x﹣4,
联立方程组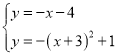 ,
,
解得![]() 或
或![]() ,
,
∴G(﹣1,﹣3),
当D点与F或G重合时,S△EBD=S△EBO,
此时D(﹣4,0)或(﹣1,﹣3),
综上,在抛物线W或V的图象上存在点D,使S△EBD=S△EBO,D的坐标为(﹣3,3)或(﹣4,0)或(﹣1,﹣3).

 阅读快车系列答案
阅读快车系列答案