题目内容
【题目】如图1,O为平面直角坐标系的原点,点A坐标为(4,0),同时将点A,O分别向上平移2个单位,再向左平移1个单位,得到对应点B,C.

(1)求四边形OABC的面积;
(2)在y轴上是否存在一点M,使△MOA的面积与四边形OABC的面积相等?若存在这样一点,求出点M的坐标,若不存在,请说明理由;
(3)如图2,点P在OA边上,且∠CBP=∠CPB,Q是AO延长线上一动点,∠PCQ的平分线CD交BP的延长线于点D,在点Q运动的过程中,求∠D和∠CQP的数量关系.
【答案】(1)8(2)M(0,4)或(0,-4)(3)∠CQP=2∠D
【解析】
(1)首先证明四边形OABC是平行四边形,理由平行四边形的面积公式计算即可;
(2)存在.如图1中,设M(0,m),根据绝对值方程即可解决问题;
(3)结论:∠CQP=2∠D.如图3中,延长CP到K.首先证明∠DPQ=∠DPK,设∠DPQ=∠DPK=x,∠DCQ=∠DCP=y,构建方程组即可解决问题;
(1)如图1中,由题意B(3,1),C(-1,2),
∴BC∥OA,BC=OA,
∴四边形ABCO是平行四边形.
∴S平行四边形ABCD=4×2=8.
(2)存在.理由:如图1中,设M(0,m)
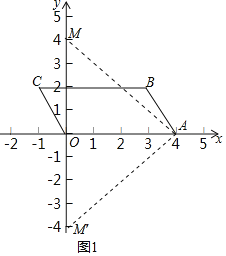
由题意S△AOM=8,
∴![]() ×4×|m|=8
×4×|m|=8
∴m=±4,
∴M(0,4)或(0,-4).
(3)结论:∠CQP=2∠D.
理由:如图3中,延长CP到K.
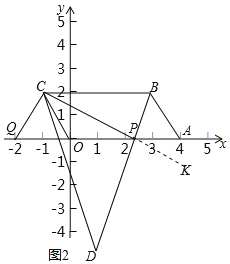
∵BC∥OA,
∴∠CBP=∠DPQ,
∵∠CBP=∠CPB,∠CPB=∠DPK,
∴∠DPQ=∠DPK,设∠DPQ=∠DPK=x,∠DCQ=∠DCP=y,
则有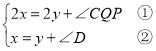 ,
,
①-2×②得到∠CQP=2∠D.

【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?








