ΧβΡΩΡΎ»ί
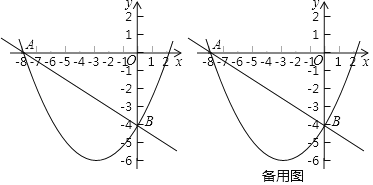
ΓΨΧβΡΩΓΩ»γΆΦΔΌ“―÷ΣœΏΕΈCDΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΈΣyΘΫ©¹![]() x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
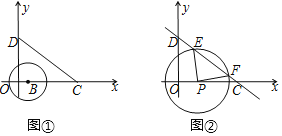
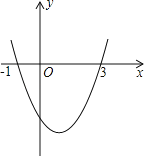
Θ®1Θ©»τ“‘ΒψBΘ®1Θ§0Θ©ΈΣ‘≤–ΡΒΡΓ―BΑκΨΕΈΣrΘ§Γ―B”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§‘ρr¬ζΉψΓΓ ΓΓΘ°
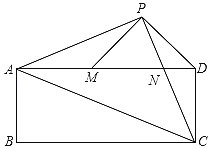
Θ®2Θ©»γΆΦΔΎΘ§»γΙϊΒψP¥”Θ®©¹5Θ§0Θ©≥ωΖΔΘ§“‘1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ίx÷αœρ”“Ής‘»ΥΌ‘ΥΕ·Θ§Β±‘ΥΕ· ±ΦδΒΫtΟκ ±Θ§“‘ΒψPΈΣ‘≤–ΡΓΔ![]() tΗωΒΞΈΜ≥ΛΕ»ΈΣΑκΨΕΒΡ‘≤P”κœΏΕΈCDΥυ‘Ύ÷±œΏ”–ΝΫΗωΫΜΒψΘ§Ζ÷±πΈΣΒψEΓΔFΘ§«“ΓœEPFΘΫ2ΓœOCDΘ§«σ¥Υ ±tΒΡ÷ΒΘ°
tΗωΒΞΈΜ≥ΛΕ»ΈΣΑκΨΕΒΡ‘≤P”κœΏΕΈCDΥυ‘Ύ÷±œΏ”–ΝΫΗωΫΜΒψΘ§Ζ÷±πΈΣΒψEΓΔFΘ§«“ΓœEPFΘΫ2ΓœOCDΘ§«σ¥Υ ±tΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©rΘΫ![]() Μρ3ΘΦrΓή
Μρ3ΘΦrΓή![]() ΘΜΘ®2Θ©tΘΫ
ΘΜΘ®2Θ©tΘΫ![]() sΜρ
sΜρ![]() s ±Θ§¬ζΉψΧθΦΰΘ°
s ±Θ§¬ζΉψΧθΦΰΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Ζ÷ΝΫ÷÷«ι–ΈΘΚΔΌœύ«–ΘΜΔΎ”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§Ζ÷±π«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©Ζ÷ΝΫ÷÷«ι–ΈΖ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
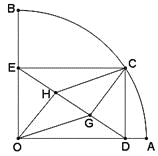
ΫβΘΚΘ®1Θ©»γΆΦΔΌ÷–Θ§ΉςBHΓΆCD”ΎHΘ°
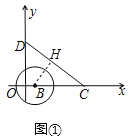
ΓΏ÷±œΏyΘΫ©¹![]() x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
ΓύCΘ®4Θ§0Θ©Θ§DΘ®0Θ§3Θ©Θ§
ΓύODΘΫ3Θ§OCΘΫ4Θ§
ΓύCDΘΫ![]() ΘΫ5Θ§
ΘΫ5Θ§
ΓΏBΘ®1Θ§0Θ©Θ§
ΓύOBΘΫ1Θ§BCΘΫ3Θ§
ΓΏΓœBCHΘΫΓœDCOΘ§ΓœBHCΘΫΓœCODΘΫ90ΓψΘ§
ΓύΓςBCHΓΉΓςDCOΘ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύBHΘΫ![]() Θ§
Θ§
ΓύΒ±rΘΫ![]() ±Θ§÷±œΏCD”κΓ―Bœύ«–Θ§÷Μ”–“ΜΗωΫΜΒψΘ§
±Θ§÷±œΏCD”κΓ―Bœύ«–Θ§÷Μ”–“ΜΗωΫΜΒψΘ§
ΓΏBDΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύΒ±3ΓήrΘΦ![]() ±Θ§Γ―B”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§
±Θ§Γ―B”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§
Ι ¥πΑΗΈΣΘΚrΘΫ![]() Μρ3ΘΦrΓή
Μρ3ΘΦrΓή![]() Θ°
Θ°
Θ®2Θ©ΔΌ»γΆΦΔΎ÷–Θ§Β±ΒψP‘ΎœΏΕΈOC…œ ±Θ§ΉςPHΓΆEF”ΎHΘ°
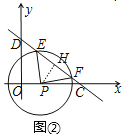
ΓΏΓœEPFΘΫ2ΓœOCDΘ§
ΓΏPEΘΫPFΘ§PHΓΆEFΘ§
ΓύΓœEPHΘΫΓœFPHΘ§
ΓύΓœHPFΘΫΓœOCDΘ§
ΓΏPFΘΫ![]() tΘ§
tȧ
ΓύPHΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§
tȧ
PCΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§
tȧ
Γύt+![]() tΘΫ9Θ§
tΘΫ9Θ§
ΓύtΘΫ![]() Θ°
Θ°
ΔΎ»γΆΦΔΎ©¹1÷–Θ§Β±ΒψP‘ΎOC ΒΡ―”≥ΛœΏ…œ ±Θ§ΉςPHΓΆEF”ΎHΘ°
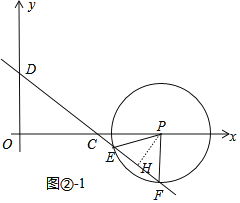
Ά§Ζ®Ω…÷ΣPFΘΫ![]() tΘ§PHΘΫ
tΘ§PHΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§PCΘΫ
tΘ§PCΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§
tȧ
Ω…ΒΟΘΚtΘΫ![]() t+9Θ§
t+9Θ§
tΘΫ![]()
Ήέ…œΥυ ωΘ§tΘΫ![]() sΜρ
sΜρ![]() s ±Θ§¬ζΉψΧθΦΰΘ°
s ±Θ§¬ζΉψΧθΦΰΘ°

 ÷ά≠ ÷»Ϊ”≈ΝΖΩΦΨμœΒΝ–¥πΑΗ
÷ά≠ ÷»Ϊ”≈ΝΖΩΦΨμœΒΝ–¥πΑΗ