题目内容
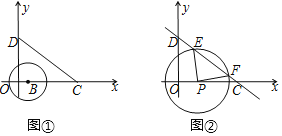
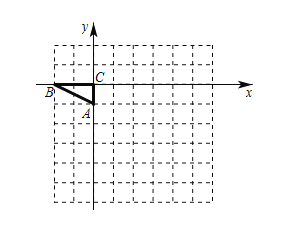
【题目】如图，平面直角坐标系中，以点C为坐标原点，点
，
，将
绕点A顺时针旋转90°．
（1）在图中画出旋转后的
，并写出点
、
的坐标；
（2）已知点
，在x轴上求作一点P（注：不要求写出P点的坐标），使得PD的值最小，并求出
的最小值；
（3）写出在旋转过程中，线段AB扫过的面积
【答案】（1）见解析，点
、
的坐标分别为
和
；（2）
的最小值为
；（3）
.
【解析】
（1）依据△ABC绕点A顺时针旋转90°，即可得到旋转后的△AB′C′，并写出点B′、C′的坐标；
（2）点B'与点C'关于x轴对称，连接B'D交x轴于点P，则PC′+PD的值最小，依据勾股定理即可得到PC′+PD的最小值；
（3）依据扇形的面积计算公式，即可得到线段AB扫过的面积．
解：（1）如图所示，
即为所求，点、的坐标分别为
和
；
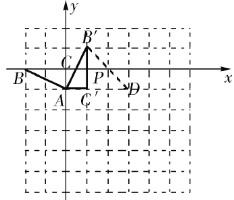
（2）如图所示，点与点关于x轴对称，连接
交x轴于点P，则的值最小，的最小值为：
；
（3）线段AB扫过的面积为：
.
练习册系列答案
相关题目
【题目】某水果店以10元/千克的价格收购一批农产品进行销售,经过市场调查获得部分数据如下表：
销售价格x(元/千克) | 10 | 13 | 16 | 19 | 22 | |
日销售量y(千克) | 100 | 85 | 70 | 55 | 40 |
(1)请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定y与x之间的函数表达式；
(2)若该水果店要获得375元的日销售利润，销售单价x应定为多少元？
(3)该水果店应该如何确定这批水果的销售价格，才能使日销售利润W最大？并求出最大利润．
