题目内容
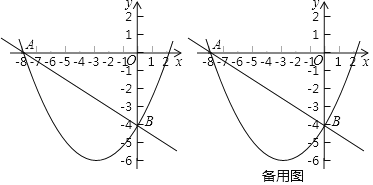
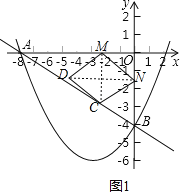
【题目】在平面直角坐标系中,抛物线y=ax2+bx﹣4经过点A(﹣8,0),对称轴是直线x=﹣3,点B是抛物线与y轴交点,点M、N同时从原点O出发,以每秒1个单位长度的速度分别沿x轴的负半轴、y的负半轴方向匀速运动,(当点N到达点B时,点M、N同时停止运动).过点M作x轴的垂线,交直线AB于点C,连接CN、MN,并作△CMN关于直线MC的对称图形,得到△CMD.设点N运动的时间为t秒,△CMD与△AOB重叠部分的面积为S.
(1)求抛物线的函数表达式;
(2)当0<t<2时,
①求S与t的函数关系式.
②直接写出当t=_____时,四边形CDMN为正方形.
(3)当点D落在边AB上时,过点C作直线EF交抛物线于点E,交x轴于点F,连接EB,当S△CBE:S△ACF=1:3时,直接写出点E的坐标为______.
【答案】(1)y=![]() x2+
x2+![]() x﹣4;(2)①S=﹣
x﹣4;(2)①S=﹣![]() t2+2t;②
t2+2t;②![]() ;(3)(﹣4,﹣6)或(﹣2,﹣6).
;(3)(﹣4,﹣6)或(﹣2,﹣6).
【解析】
(1)抛物线y=ax2+bx﹣4经过点A(﹣8,0),对称轴是直线x=﹣3,则抛物线与x轴另外一个交点坐标为:(2,0),则抛物线的表达式为:y=a(x+8)(x﹣2)=a(x2+6x﹣16),根据x=0时y=-4可得﹣16a=﹣4,解得:a=![]() ,即可求解;(2)①根据OM=ON=t可得AM=8﹣t,由MC∥y轴,根据平行线分线段成比例定理可得
,即可求解;(2)①根据OM=ON=t可得AM=8﹣t,由MC∥y轴,根据平行线分线段成比例定理可得![]() ,可得MC=
,可得MC=![]() (8﹣t),进而可得S=S△MCN=
(8﹣t),进而可得S=S△MCN=![]() MC×t=﹣
MC×t=﹣![]() t2+2t;②根据MC=ND=2t,即可求解;(3)过点E、F分别作AB的垂线交AB于点G、H,利用待定系数法可得直线AB的解析式,根据对称性质可得DM=MN=
t2+2t;②根据MC=ND=2t,即可求解;(3)过点E、F分别作AB的垂线交AB于点G、H,利用待定系数法可得直线AB的解析式,根据对称性质可得DM=MN=![]() t,可证明△DMN是等腰直角三角形,可得DN=
t,可证明△DMN是等腰直角三角形,可得DN=![]() MN,即可求出t值,可得点C(﹣2,﹣3),即可得出AC=3BC,根据S△CBE:S△ACF=1:3,可得EG=FH,利用AAS可证明△FHC≌△EGC,可得FC=EC,故点C是EF的中点,设F(m,0),根据中点坐标公式可用m表示出E点坐标,代入二次函数解析式即可求出m的值,可得E点坐标.
MN,即可求出t值,可得点C(﹣2,﹣3),即可得出AC=3BC,根据S△CBE:S△ACF=1:3,可得EG=FH,利用AAS可证明△FHC≌△EGC,可得FC=EC,故点C是EF的中点,设F(m,0),根据中点坐标公式可用m表示出E点坐标,代入二次函数解析式即可求出m的值,可得E点坐标.
(1)∵抛物线y=ax2+bx﹣4经过点A(﹣8,0),对称轴是直线x=﹣3,
∴抛物线与x轴另外一个交点坐标为(2,0),
∴抛物线的表达式为:y=a(x+8)(x﹣2)=a(x2+6x﹣16),
∵点B是抛物线与y轴交点,
∴B(0,4),
∴﹣16a=﹣4,
解得:a=![]() ,
,
∴抛物线的表达式为:y=![]() x2+
x2+![]() x﹣4.
x﹣4.
(2)如图1,①∵OM=ON=t,
∴AM=8﹣t,
∵MC∥y轴,
∴![]() ,即
,即![]() ,
,
解得:MC=![]() (8﹣t),
(8﹣t),
∵△CMN与△CMD关于直线MC对称,
∴S△CMD=S△CMN,
∵0<t<2,
∴S=S△MCN=![]() MC×t=﹣
MC×t=﹣![]() t2+2t.
t2+2t.
②四边形CDMN为正方形时,MN=![]() ,
,
∴MC=ND=![]() =2t,
=2t,
∴MC=![]() (8﹣t)=2t,
(8﹣t)=2t,
解得:t=![]() ,
,
故答案为:![]()
(3)设直线AB的解析式为y=kx+b,
∵A(-8,0),B(0,-4),
∴![]() ,
,
解得: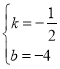 ,
,
∴直线AB的表达式为:y=﹣![]() x﹣4,
x﹣4,
如图2,当点D在AB上时,设点M(﹣t,0),
∴N(0,-t),
当y=-t时,﹣![]() x﹣4=-t,
x﹣4=-t,
解得:x=2t-8,
∴点D(2t﹣8,﹣t),
∴DN=8-2t,
∵OM=ON=t,
∴MN=![]() t,∠OMN=∠ONM=45°,
t,∠OMN=∠ONM=45°,
∵MC⊥x轴,
∴∠CMN=45°,
∵△CMN与△CMD关于直线MC对称,
∴∠DMC=∠CMN=45°,
∴∠DMN=90°,
∴△DMN是等腰直角三角形,
∴DN=![]() MN,即8-2t=
MN,即8-2t=![]() ×
×![]() t,
t,
解得:t=2,
∵点C在直线AB上,MC⊥x轴,
∴当x=-2时,y=-![]() ×(-2)-4=-3,
×(-2)-4=-3,
∴点C(﹣2,﹣3),
∴AC=![]() =3
=3![]() ,BC=
,BC=![]() =
=![]() ,
,
∴AC=3BC,
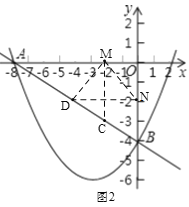
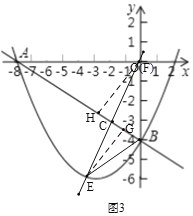
如图3,过点E、F分别作AB的垂线交AB于点G、H,
∵S△CBE:S△ACF=1:3,
∴![]() AC·FH=3×
AC·FH=3×![]() BC·EG,即
BC·EG,即![]() ×3BC·FH=3×
×3BC·FH=3×![]() BC·EG,
BC·EG,
∴EG=FH,
∵FH⊥AB,EG⊥AB,
∴∠FHC=∠EGC=90°,
在△FHC和△EGC中,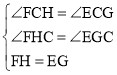 ,
,
∴△FHC≌△EGC,
∴FC=EC,
∴点C是EF的中点,设点F(m,0),E(x,y),
∵点C(﹣2,﹣3),
∴![]() ,
,![]() ,
,
解得:x=-4-m,y=-6,
∴点E(﹣4﹣m,﹣6),
把点E的坐标代入抛物线表达式得:-6=![]() (-4-m)2+
(-4-m)2+![]() (-4-m)-4,
(-4-m)-4,
解得:m=0或﹣2,
当m=0时,-4-m=-4,点E坐标为(-4,-6),
当m=-2时,-4-m=-2,点E坐标为(-2,6),
综上所述:点E的坐标为:(﹣4,﹣6)或(﹣2,﹣6),
故答案为:(﹣4,﹣6)或(﹣2,﹣6).

 阅读快车系列答案
阅读快车系列答案【题目】某水果店以10元/千克的价格收购一批农产品进行销售,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 10 | 13 | 16 | 19 | 22 | |
日销售量y(千克) | 100 | 85 | 70 | 55 | 40 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定y与x之间的函数表达式;
(2)若该水果店要获得375元的日销售利润,销售单价x应定为多少元?
(3)该水果店应该如何确定这批水果的销售价格,才能使日销售利润W最大?并求出最大利润.