��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P (x��y)������Q������Ϊ(ax+y��x+ay)�� ����aΪ��������Ƶ�Q�ǵ�P����a��������"�����磬��P(1��4)����3��������"ΪQ (3��1+4��1+3��4)�� ��Q (7��13)��

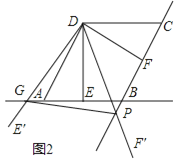
(1)��֪��A (-2��6)����![]() �����������ǵ�A1����B����2������������B1 (3�� 3)�� ���A1�͵�B�����꣺
�����������ǵ�A1����B����2������������B1 (3�� 3)�� ���A1�͵�B�����꣺
(2)��֪��M (m-1�� 2m)����-3��������"Mλ���������ϣ���M������
���𰸡���1��A1 (5�� 1)��![]() ����2��
����2��![]() (
(![]() ��0)��
��0)��![]() (0��-16).
(0��-16).
��������
��1�����ݹ�����Ķ��壬��ϵ�����꼴�ɵó����ۣ�
��2���ȱ�ʾ����M��m-1��2m���ġ�-3�������㡱M�䣬Ȼ������������⼴�����M������꣮
(1) ����A(-2�� 6)����![]() �����������ǵ�A��
�����������ǵ�A��
��A (![]() ��
��![]() )�� ��A1 (5�� 1).
)�� ��A1 (5�� 1).
���B(x�� y)��
����B����2��������"��B (3�� 3)��
��![]() ��
��
���![]() ����
����![]() ��
��
(2) ����M(m-1�� 2m) ����- 3����������ΪM (-3 (m-1) +2m�� m-1+ (-3) ��2m)����![]() (-m+3�� -5m-1)��
(-m+3�� -5m-1)��
��![]() λ��x���ϣ�.m-1-6m= =0��ã�
λ��x���ϣ�.m-1-6m= =0��ã�![]() ��
��
��-3 (m-1) +2m=![]() ��
��
![]() ��
��
��![]() λ��y���ϣ���.-3 (m-1) +2m=0����ã� m=3��
λ��y���ϣ���.-3 (m-1) +2m=0����ã� m=3��
��![]() ��
��![]() .
.
����������![]() ��������
��������![]() (
(![]() ��0)��
��0)��![]() (0��-16).
(0��-16).

 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�����Ŀ��ij���Լ����μ��п���5000�����б�ҵ��������һ�������������飬���Ƴ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��һ���֣�
�����ͼ����Ϣ�ش��������⣺
���� | Ƶ�����ˣ� | Ƶ�� |
4.0��x��4.3 | 20 | 0.1 |
4.3��x��4.6 | 40 | 0.2 |
4.6��x��4.9 | 70 | 0.35 |
4.9��x��5.2 | a | 0.3 |
5.2��x��5.5 | 10 | b |
��1�����ε��������Ϊ________����������Ϊ_______��
��2����Ƶ���ֲ����У�a=______��b=______������Ƶ���ֲ�ֱ��ͼ����������
��3����������4.6���ϣ���4.6����������������������Ϣ����ȫ�����б�ҵ��������������ѧ���ж����ˣ�