Question

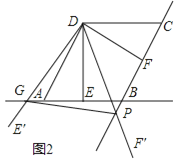
【题目】如图，在菱形ABCD中，AB=2，∠BAD=60°，过点D作DE⊥AB于点E，DF⊥BC于点F．将∠EDF以点D为旋转中心旋转，其两边DE′，DF′分别与直线AB，BC相交于点G，P，连接GP，当△DGP的面积等于3时，求旋转角的大小并指明旋转方向．

Answer 1

【答案】当∠EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积等于3.

【解析】

分∠EDF顺时针旋转和逆时针旋转两种情况，根据旋转变换的性质解答即可．

解：∵AB∥DC，∠BAD=60°，

∴∠ADC=120°.

又∠ADE=∠CDF=30°，

∴∠EDF=60°.

当∠EDF顺时针旋转时，由旋转的性质可知，∠EDG=∠FDP，∠GDP=∠EDF=60°.

在Rt△ADE中，∠ADE=30°,AE=AD=1.

∴DE==.

同理，DF=.

在△DEG和△DFP中，∠EDG=∠FDP，DE＝DF，∠DEG＝∠DFP=90°，

∴△DEG≌△DFP.

∴DG=DP.

∴△DGP为等边三角形.

易得S△DGP=DG2.

由DG2=3，又DG＞0，解得DG=2.

在Rt△DEG中，=,

∴∠DGE=30°.

∴∠EDG=60°.

∴当顺时针旋转60°时，△DGP的面积等于3.

同理可得，当逆时针旋转60°时，△DGP的面积也等于3.

综上所述，当∠EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积等于3.