Question

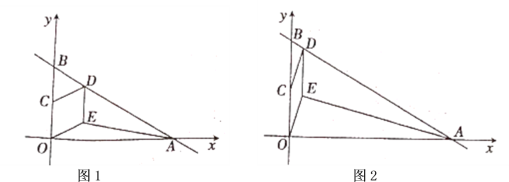
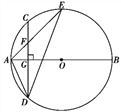
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=;④S△ADF=6.

其中正确结论的个数是(　　)

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】A

【解析】分析：①利用垂径定理可知，可知∠ADF=∠AED，结合公共角可证明△ADF∽△AED；②结合CF=2，且，可求得DF=6，且CG=DG，可求得FG=2；③在Rt△AGF中可求得AG，在Rt△AGD中可求得tanADG=，且∠E=∠ADG，可判断出③；④可先求得S△ADF，再求得△ADF∽△AED的相似比，可求出S△ADE=7．

详解：①∵AB为直径，AB⊥CD，

∴，

∴∠ADF=∠AED，且∠FAD=∠DAE，

∴△ADF∽△AED，

∴①正确；

②∵AB为直径，AB⊥CD，

∴CG=DG，

∵，且CF=2，

∴FD=6，

∴CD=8，

∴CG=4，

∴FG=CG-CF=4-2=2，

∴②错误；

③在Rt△AGF中，AF=3，FG=2，

∴AG=，且DG=4，

∴tan∠ADG=，

∵∠E=∠ADG，

∴tan∠E=，

∴③错误；

④在Rt△ADG中，AG=，DG=4，

∴AD=，

∴，

∴△ADF∽△AED中的相似比为，

∴，

在△ADF中，DF=6，AG=，

∴S△ADF=DFAG=×6×=3，

∴，

∴S△ADE=7，

∴④错误；

∴正确的有①一个．

故选：A．