题目内容
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
【答案】(1)![]() ;(2)点
;(2)点![]() 所对应的数为
所对应的数为![]() 或
或![]() ;(3)设点P所表示的数为p,当-6≤p≤-1时,
;(3)设点P所表示的数为p,当-6≤p≤-1时,![]() 最小,且最小值为9
最小,且最小值为9
【解析】
(1)根据平方和绝对值的非负性即可求出a、b的值;
(2)先求出AB的值,设点C表示的数为c,然后根据点C的位置分类讨论,分别画出图形,利用含c的式子表示出AC和BC,列出对应的方程即可求出;
(3)根据中点公式求出点D所表示的数,设点P所表示的数为p,根据点P与点O的相对位置分类讨论,画出相关的图形,分析每种情况下![]() 取最小值时,点P的位置即可.
取最小值时,点P的位置即可.
解:(1)∵![]() ,
,![]()
∴![]()
解得:![]() ;
;
(2)由(1)可得:AB=4-(-6)=10
设点C表示的数为c
①当点C在点B左侧时,如下图所示

∴AC=4-c,BC=-6-c
∵![]()
∴![]()
解得:c=![]() ;
;
②当点C在线段AB上时,如下图所示:
![]()
此时AC+BC=AB
故不成立;
③当点C在点A右侧时,如下图所示

∴AC=c-4,BC= c -(-6)=c+6
∵![]()
∴![]()
解得:c=![]() ;
;
综上所述:点![]() 所对应的数为
所对应的数为![]() 或
或![]() ;
;
(3)∵点D为AB的中点
所以点D表示的数为![]()
设点P所表示的数为p
①当点P在点O左侧时,如以下三个图所示,此时PA-PO=AO=4
∴![]()
即当![]() 取最小值时,
取最小值时,![]() 也最小
也最小
由以下三个图可知:当点P在线段BD上时,![]() 最小,此时
最小,此时![]()



∴此时![]()
即当-6≤p≤-1时,![]() 最小,且最小值为9;
最小,且最小值为9;
②当点P在点O右侧时,如以下两个图所示,此时PB-PO=OB=6
∴![]()
即当![]() 取最小值时,
取最小值时,![]() 也最小
也最小
由以下两个图可知:当点P在线段OA上时,![]() 最小,此时
最小,此时![]()


∴此时![]()
即当0≤p≤4时,![]() 最小,且最小值为11;
最小,且最小值为11;
综上所述:当-6≤p≤-1时,![]() 最小,且最小值为9.
最小,且最小值为9.

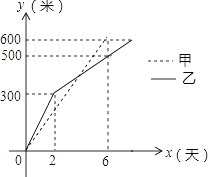
【题目】端午节放假期间,某学校计划租用![]() 辆客车送
辆客车送![]() 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
甲种客车 | 乙种客车 | |
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
(1)求出![]() (元)与
(元)与![]() (辆)之间函数关系式;
(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.