Question

【题目】直线与轴、轴分別交于、两点，是的中点，是线段上一点.

(1)求点、的坐标；

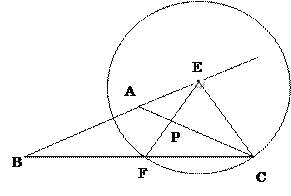
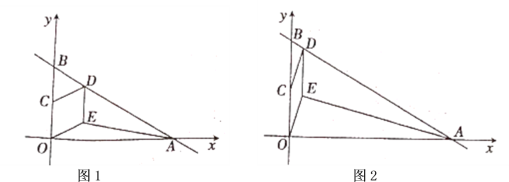
(2)若四边形是菱形，如图1，求的面积；

(3)若四边形是平行四边形，如图2，设点的横坐标为，的面积为，求关于的函数关系式.

Answer 1

【答案】（1），；（2）；（3）当时， ；当 时，

【解析】

（1）当x=0时，y=4，当y=0时，x=4，即可求点A，点B坐标；
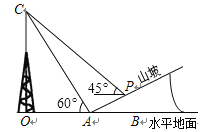
（2）过点D作DH⊥BC于点H，由锐角三角函数可求∠ABO=60°，由菱形的性质可得OC=OD=DE=2，可证△BCD是等边三角形，可得BD=2，可求点D坐标，即可求△AOE的面积；
（3）分两种情况讨论，利用平行四边形的性质和三角形面积公式可求解．

解：（1）∵直线y=-x+4与x轴、y轴分别交于A、B两点，
∴当x=0时，y=4，
当y=0时，x=4
∴点A（4，0），点B（0，4）
（2）如图1，过点D作DH⊥BC于点H，

，

∴tan∠ABO＝

为的中点，四边形为菱形，

为等边三角形

∴BD=2

∵DH⊥BC，∠ABO=60°
∴BH=1，HD=BH=
∴当x=时，y=3
∴D（，3）
∴S△AOE=×4×（3-2）=2

(3)由是线段上一点，设

四边形是平行四边形

当，即时

当，即时