题目内容
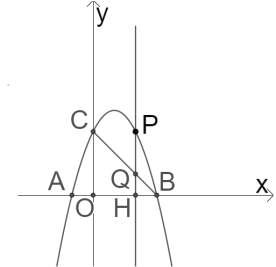
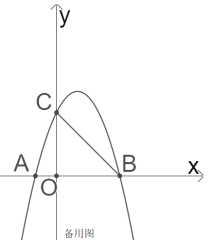
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C(0,3),点P是抛物线在第一象限上的一点,过点P作PH⊥x轴,垂足为H,交线段BC于点Q.
(1)求抛物线对应的函数表达式;
(2)当PQ=2QH时,求点P的坐标;
(3)当PH最大时,连接AP,AP与BC交于点D,点F是第一象限内一点,且∠AFC=45°,点G在抛物线上,直线FG、FC分别与直线PH交于点M、N.当三角形ABD相似三角形FMN时,求点G的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求解即可;
(2)先根据二次函数的解析式求出点B的坐标,再利用待定系数法求出直线BC的解析式,然后根据![]() 建立等式求解即可;
建立等式求解即可;
(3)在(2)的基础上,先利用二次函数的性质求出点P的坐标,在利用二次函数的性质、正切函数值得出![]() ,然后根据相似三角形的性质分三种情况:①当
,然后根据相似三角形的性质分三种情况:①当![]() 时、②当
时、②当![]() 时、③当
时、③当![]() 时,先分别利用相似三角形的性质确认点F在直线PA上,再利用相似三角形的性质得出点N的坐标,从而可得直线CN的解析式,然后联立直线PA、CN的解析式可求出点F的坐标,进而利用待定系数法可求出直线FG的解析式,最后联立二次函数与直线FG的解析式即可得.
时,先分别利用相似三角形的性质确认点F在直线PA上,再利用相似三角形的性质得出点N的坐标,从而可得直线CN的解析式,然后联立直线PA、CN的解析式可求出点F的坐标,进而利用待定系数法可求出直线FG的解析式,最后联立二次函数与直线FG的解析式即可得.
(1)将![]() 代入
代入![]() 得
得![]()
解得![]()
故抛物线对应的函数表达式为![]() ;
;
(2)对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]()
则点B的坐标为![]()
设直线BC的解析式为![]()
将![]() 代入得
代入得![]() ,解得
,解得![]()
则直线BC的解析式为![]()
设![]() ,则
,则![]() ,
,![]() ,且
,且![]()
因此有![]() ,
,![]()
由![]() 得:
得:![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
此时,![]()
故点P的坐标为![]() ;
;
(3)由(2)可知,![]()
由二次函数的性质得:当![]() 时,PH取得最大值,最大值为4
时,PH取得最大值,最大值为4
则![]() ,
,![]()
设直线PA的解析式为![]()
将![]() ,
,![]() 代入得
代入得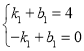 ,解得
,解得![]()
则直线PA的解析式为![]()
联立![]() ,解得
,解得![]()
![]()
![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() ,
,![]()
![]()
由两点之间的距离公式得:![]()
![]()
![]()
由二次函数的对称性可知,![]()
![]() ,
,![]()
![]()
在![]() 中,
中,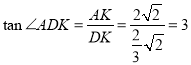
在![]() 中,
中,![]()
![]() ,即
,即![]()
根据相似三角形的性质,分以下三种情况:
①当![]() 时
时
![]()
![]()
则点F不可能位于第一象限,不符题意
②如图1,当![]() 时
时
![]()
![]()
设AF与BC的交点为点Q
![]() 点F是第一象限内一点,且
点F是第一象限内一点,且![]()
![]() 点F在
点F在![]() 外接圆位于第一象限的弧上
外接圆位于第一象限的弧上
由圆周角定理得:![]()
又![]()
![]()
![]()
则当三角形ABD相似三角形FMN时,![]() 与
与![]() 也相似或完全重合
也相似或完全重合
![]()
![]()
![]()
![]() 与
与![]() 找不出两组对应相等的角
找不出两组对应相等的角
即![]() 与
与![]() 不可能相似,只能是完全重合
不可能相似,只能是完全重合
![]() 点Q与点D重合
点Q与点D重合
则点F在直线PA:![]() 上,
上,![]()
![]() ,即
,即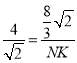
解得![]()
![]() ,即
,即![]()
设直线CN的解析式为![]()
将![]() ,
,![]() 代入得:
代入得: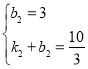 ,解得
,解得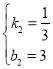
则直线CN的解析式为![]()
联立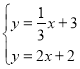 ,解得
,解得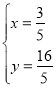
则![]()
又![]()
![]() ,即
,即![]()
则可设直线FG的解析式为![]()
点![]() 代入得
代入得![]() ,解得
,解得![]()
则直线FG的解析式为![]()
联立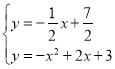 ,解得
,解得![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
则此时点G的坐标为![]() 或
或![]()
③如图2,当![]() 时
时
![]()
![]()
![]()
同②可得:点F在直线PA:![]() 上,
上,![]() ,
,![]()
又![]()
![]() 可设直线FG的解析式为
可设直线FG的解析式为![]()
将点![]() 代入得:
代入得:![]() ,解得
,解得![]()
则直线FG的解析式为![]()
联立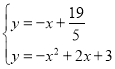 ,解得
,解得![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
则此时点G的坐标为![]() 或
或![]()
综上,点G的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】![]() 年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
商品 价格 | 甲 | 乙 |
进件(元 |
|
|
售价(元 |
|
|
该店有一批用![]() 元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共
元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共![]() 元.[毛利润
元.[毛利润![]() (售价
(售价![]() 进价)
进价)![]() 销售量]
销售量]


(1)该店库存的甲、乙两种手持红外测温枪分别为多少个?
(2)根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量.已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的![]() 倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过
倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过![]() 元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.
元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.
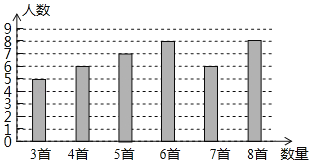
【题目】某校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数.
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.