Question

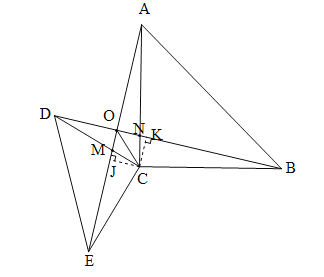
【题目】如图，在∠△ACB和△DCE中，AC＝BC，CD＝CE，∠ACB＝∠DCE＝90°，连接AE、BD交于点O，AE与DC交于点M，BD与AC交于点N．

(1)试判断AE、BD之间的关系，并说明理由；

(2)连接CO，则下面两个结论中选择你认为正确的一个加以说明①射线CO平分∠ACD ②射线OC平分∠BOE

Answer 1

【答案】（1）AE=BD且AE⊥BD；（2）②正确．

【解析】

（1）根据∠ACB=∠DCE，可得∠DCB=∠ACE，已知AC=BC，CD=CE，可得△ACE≌△BCD，则AE=BD，∠CEA=∠BDC，根据三角形内角和定理可得∠DOM=∠ECM=90°，即有AE⊥BD；

（2）过C作CJ⊥AE于J，CK⊥DB于K．由△ACE≌△BCD，得到S△ACE=S△BCD，从而得到CJ=CK．由角平分线的判定即可得到结论．

（1）AE=BD且AE⊥BD．理由如下：

∵∠ACB=∠DCE，∴∠ACB+∠DCA=∠DCE+∠DCA，即∠DCB=∠ACE．

∵AC=BC，CD=CE，∴△ACE≌△BCD（SAS），∴AE=BD，∠CEA=∠BDC．

∵∠CME=∠DMO，∴∠DOM=∠ECM=90°，∴AE⊥BD，∴AE=BD且AE⊥BD．

（2）②正确．理由如下：

过C作CJ⊥AE于J，CK⊥DB于K．

∵△ACE≌△BCD，∴S△ACE=S△BCD，∴×AE×CJ=×DB×CK．

∵AE=DB，∴CJ=CK．

∵CJ⊥AE，CK⊥DB，∴OC平分∠BOE．故②正确．