题目内容
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 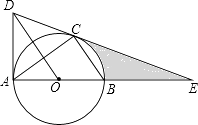
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=6,CE=2 ![]() . ①求⊙O的半径
. ①求⊙O的半径
②求线段CE,BE与劣弧 ![]() 所围成的图形的面积(结果保留根号和π)
所围成的图形的面积(结果保留根号和π)
【答案】
(1)解:连结OC,如图,
∵AD为⊙O的切线,
∴AD⊥AB,
∴∠BAD=90°,
∵OD∥BC,
∴∠1=∠3,∠2=∠4,
∵OB=OC,
∴∠3=∠4,
∴∠1=∠2,
在△OCD和△OAD中, 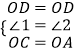 ,
,
∴△AOD≌△COD(SAS);
∴∠OCD=∠OAD=90°,
∴OC⊥DE,
∴DE是⊙O的切线
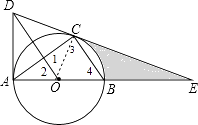
(2)解:①设半径为r,则OE=AE﹣OA=6﹣r,OC=r,
在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2 ![]() )2=(6﹣r)2,解得r=2,
)2=(6﹣r)2,解得r=2,
②∵tan∠COE= ![]() =
= ![]() =
= ![]() ,
,
∴∠COE=60°,
∴S阴影部分=S△COE﹣S扇形BOC
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]()
=2 ![]() ﹣
﹣ ![]() π
π
【解析】(1)连结OC,如图,先根据切线的性质得∠BAD=90°,再根据平行线的性质,由OD∥BC得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,接着证明△AOD≌△COD,得到∠OCD=∠OAD=90°,于是可根据切线的判定定理得到DE是⊙O的切线;(2)①设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中利用勾股定理得到r2+(2 ![]() )2=(6﹣r)2 , 解得r;②利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
)2=(6﹣r)2 , 解得r;②利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
【考点精析】掌握三角形的外接圆与外心和切线的性质定理是解答本题的根本,需要知道过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱进价和售价如下表所示:
饮料 | 果汁饮料 | 碳酸饮料 |
进价(元/箱) | 55 | 36 |
售价(元/箱) | 63 | 42 |
设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价﹣总进价).
(1)求总利润w关于x的函数关系式;
(2)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.