Question

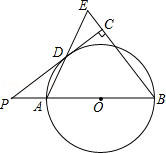
【题目】已知：如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx+3交y轴于点A，交x轴正半轴于点C（3，0），交x轴负半轴于点B（﹣1，0），∠ACB=45°．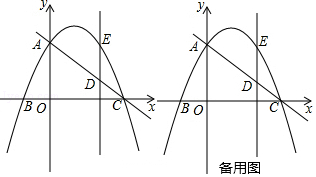

（1）求此抛物线的解析式；
（2）点D为线段AC上一点，且AD=2CD，过点D作DE∥y轴，交抛物线一点E，点P为x轴上方抛物线的一点，设点P的横坐标为t，△PDE的面积为s，求s与t之间的函数关系式，并直接写出t的范围；
（3）在（2）的条件下，过点P作PF∥DE交直线AC于点F，是否存在点P，使以点P、F、E、D为顶点的平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：把B（﹣1，0），C（3，0），代入函数解析式得：

，

解得：

故抛物线解析式为：y=﹣x2+2x+3

（2）

解：设DE与x轴交于点H，

∵DE∥y轴，AD=2CD，

∴ = = ，

∴DH=CH=1，

∴D（2，1），

∵点E在抛物线上，

∴E（2，3），

∵点P为x轴上方抛物线上的一点，设点P的横坐标为t，

∴﹣1＜t＜3，

∵△PDE的面积为S，

∴ DE|t﹣2|=S，

∴S=|t﹣2|（﹣1＜t＜3），

即当﹣1＜t＜2时，S=2﹣t，

当2＜t＜3时，S=t﹣2

（3）

解：如图所示：设直线AC的解析式为y=kx+b，

∴ ，

解得： ，

∴直线AC的解析式为y=﹣x+3，

假设抛物线上存在点P，使以点P、F、E、D为顶点的四边形为平行四边形，

设点P坐标为（h，﹣h2+2h+3），

∵PF∥DE，

∴PF=DE，

∴F（h，﹣h+3），

∴﹣h2+2h+3﹣（﹣h+3）=2，

∴h2﹣3h+2=0，

∴h1=1，h2=2，

∴抛物线上存在点P，使以点P、F、E、D为顶点的四边形为平行四边形，点P的坐标为（1，4）或（2，3）．

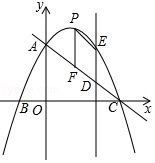
【解析】（1）直接利用点B，C坐标，利用待定系数法求出函数解析即可；（2）由AD=2CD，DE∥y轴，得出D，E两点的坐标，根据三角形的面积公式即可得出S与t之间的函数关系式，根据B，C两点坐标直接写出t的取值范围；（3）假设抛物线上存在点P，使以点P、F、E、D为顶点的四边形为平行四边形，求出直线AC的解析式，设出点P坐标，从而得出点F坐标，整理出关于h的方程，求出P点坐标，使以点P、F、E、D为顶点的四边形为平行四边形．