题目内容
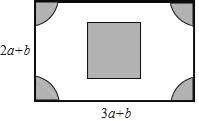
【题目】如图，有一块长（3a+b）米，宽（2a+b）米的长方形广场，园林部门要对阴影区域进行绿化，空白区域进行广场硬化，其中，四个角部分是半径为（a﹣b）米的四个大小相同的扇形，中间部分是边长为（a+b）米的正方形．
（1）用含a、b的式子表示需要硬化部分的面积；
（2）若a=30，b=10，求出硬化部分的面积（结果保留π的形式）．
【答案】（1）需要硬化部分的面积为（3a+b）（2a+b）﹣（a+b）2﹣π（a﹣b）2；（2）当a=30，b=10，硬化部分的面积为（5400﹣400π）平方米．
【解析】
（1）用长方形的面积分别减去正方形的面积和四个扇形的面积可得到需要硬化部分的面积；
（2）把a和b的值代入（1）中的代数式中计算即可．
（1）需要硬化部分的面积＝（3a+b）（2a+b）﹣（a+b）2﹣π（a﹣b）2；
（2）当a＝30，b＝10，硬化部分的面积＝（90+10）×（60+10）﹣402﹣π×202
＝（5400﹣400π）平方米．
黄冈创优卷系列答案
【题目】菲尔兹奖是国际上有崇高声誉的一个数学奖项，下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄（岁）： 29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据，解答下列问题：
小彬按“组距为5”列出了如图的频数分布表
分组 | 频数 |
A：25～30 | |
B：30～35 | 15 |
C：35～40 | 31 |
D：40～45 | |
合计 | 56 |
（1）每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图；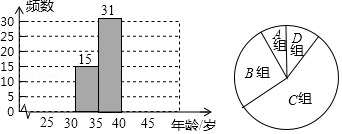 
（2）根据（1）中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征；
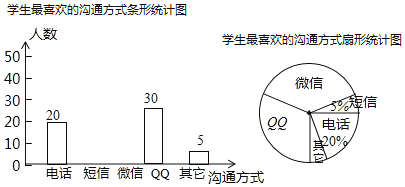
（3）在（1）的基础上，小彬又画了如图所示的扇形统计图，图中获奖年龄在30～35岁的人数约占获奖总人数的%（百分号前保留1位小数）；C组所在扇形对应的圆心角度数约为°（保留整数）