题目内容
 如图,点A是双曲线y=
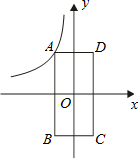
如图,点A是双曲线y= 在第二象限分支上的任意一点,点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点.若四边形ABCD的面积是8,则k的值为
在第二象限分支上的任意一点,点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点.若四边形ABCD的面积是8,则k的值为
- A.-1
- B.1
- C.2
- D.-2
D
分析:先判定出四边形ABCD是矩形,再根据反比例函数的系数的几何意义,用k表示出四边形ABCD的面积,然后求解即可.
解答:∵点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点,
∴四边形ABCD是矩形,
∵四边形ABCD的面积是8,
∴4×|-k|=8,
解得|k|=2,
又∵双曲线位于第二、四象限,
∴k<0,
∴k=-2.
故选D.
点评:本题考查了反比例函数系数的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|,利用k表示出四边形的面积是解题的关键.
分析:先判定出四边形ABCD是矩形,再根据反比例函数的系数的几何意义,用k表示出四边形ABCD的面积,然后求解即可.
解答:∵点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点,
∴四边形ABCD是矩形,
∵四边形ABCD的面积是8,
∴4×|-k|=8,
解得|k|=2,
又∵双曲线位于第二、四象限,
∴k<0,
∴k=-2.
故选D.
点评:本题考查了反比例函数系数的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|,利用k表示出四边形的面积是解题的关键.

练习册系列答案
相关题目
 如图,点A是双曲线
如图,点A是双曲线 (2013•萧山区模拟)如图,点P是双曲线
(2013•萧山区模拟)如图,点P是双曲线 如图,点P是双曲线y=
如图,点P是双曲线y=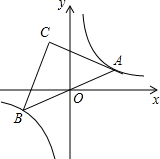 (2013•南通二模)如图,点A是双曲线y=
(2013•南通二模)如图,点A是双曲线y=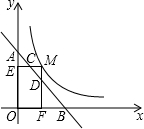 如图,点M是双曲线y=
如图,点M是双曲线y=