题目内容
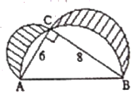
【题目】如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:
①CE=CF;
②线段EF的最小值为![]() ;
;
③当AD=2时,EF与半圆相切;
④若点F恰好落在B C上,则AD=![]() ;
;
⑤当点D从点A运动到点B时,线段EF扫过的面积是![]() .
.
其中正确结论的序号是 .

【答案】①③⑤.
【解析】试题分析:①连接CD,如图1所示,∵点E与点D关于AC对称,∴CE=CD,∴∠E=∠CDE,∵DF⊥DE,∴∠EDF=90°,∴∠E+∠F=90°,∠CDE+∠CDF=90°,∴∠F=∠CDF,∴CD=CF,∴CE=CD=CF,∴结论“CE=CF”正确;
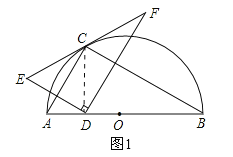
②当CD⊥AB时,如图2所示,∵AB是半圆的直径,∴∠ACB=90°,∵AB=8,∠CBA=30°,∴∠CAB=60°,AC=4,BC=![]() .∵CD⊥AB,∠CBA=30°,∴CD=
.∵CD⊥AB,∠CBA=30°,∴CD=![]() BC=
BC=![]() .根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为
.根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为![]() .∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为
.∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为![]() .∴结论“线段EF的最小值为
.∴结论“线段EF的最小值为![]() ”错误;
”错误;
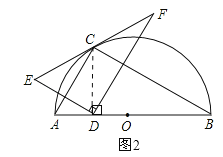
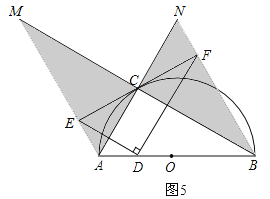
③当AD=2时,连接OC,如图3所示,∵OA=OC,∠CAB=60°,∴△OAC是等边三角形,∴CA=CO,∠ACO=60°,∵AO=4,AD=2,∴DO=2,∴AD=DO,∴∠ACD=∠OCD=30°,∵点E与点D关于AC对称,∴∠ECA=∠DCA,∴∠ECA=30°,∴∠ECO=90°,∴OC⊥EF,∵EF经过半径OC的外端,且OC⊥EF,∴EF与半圆相切,∴结论“EF与半圆相切”正确;
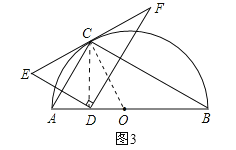
④当点F恰好落在![]() 上时,连接FB、AF,如图4所示,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴FH:FD=FC:FE,∵FC=
上时,连接FB、AF,如图4所示,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴FH:FD=FC:FE,∵FC=![]() EF,∴FH=
EF,∴FH=![]() FD,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∴BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=
FD,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∴BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=![]() AB=4,∴DB=4,∴AD=AB﹣DB=4,∴结论“AD=
AB=4,∴DB=4,∴AD=AB﹣DB=4,∴结论“AD=![]() ”错误;
”错误;
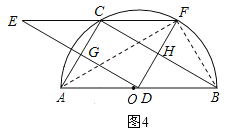
⑤∵点D与点E关于AC对称,点D与点F关于BC对称,∴当点D从点A运动到点B时,点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称,∴EF扫过的图形就是图5中阴影部分,∴S阴影=2S△ABC=2×![]() ACBC=ACBC=4×
ACBC=ACBC=4×![]() =
=![]() ,∴EF扫过的面积为
,∴EF扫过的面积为![]() ,∴结论“EF扫过的面积为
,∴结论“EF扫过的面积为![]() ”正确.
”正确.
故答案为:①③⑤.

 阅读快车系列答案
阅读快车系列答案【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?