Question

【题目】□ABCD中，AC=6，BD=10，动点P从B出发以每秒1个单位的速度沿射线BD匀速运动，动点Q从D出发以相同速度沿射线DB匀速运动，设运动时间为t秒.

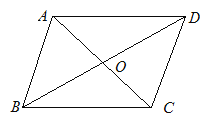
（1）当t =2时，证明以A、P、C、Q为顶点的四边形是平行四边形.

（2）当以A、P、C、Q为顶点的四边形为矩形时，直接写出t的值.

（3）设PQ=y，直接写出y与t的函数关系式.

Answer 1

【答案】(1)见解析;(2) t =2或t =8；(3) y=-2t+10（0≤t≤5时），y=2y-10（t>5时）.

【解析】（1）只需要证明四边形APCQ的对角线互相平分即可证明其为平行四边形.

（2）根据矩形的性质可知四边形APCQ的对角线相等，然后分两种情况即可解答.

（3）根据（2）中的图形，分两种情况进行讨论即可.

（1）证明：∵四边形ABCD是平行四边形，

∴OA=OC=3，OB=OD=5，

当t=2时，BP=QD=2，

∴OP=OQ=3，

∴四边形APCQ是平行四边形；

（2）t =2或t =8；

理由如下：

图一：

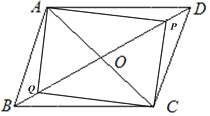
图二：

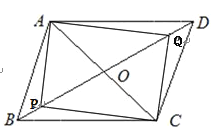
∵四边形APCQ是矩形，

∴PQ=AC=6，

则BQ=PD=2，

第一个图中，BP=6+2=8，则此时t=8；

第二个图中，BP=2，则此时t=2.

即以A、P、C、Q为顶点的四边形为矩形时，t的值为2或8；

（3）根据（2）中的两个图形可得出：

y=-2t+10（时），

y=2y-10（时）.