Question

【题目】如图，在平面直角坐标系中，点的坐标为，点是轴正半轴上一点，以为边作等腰直角三角形，使，点在第一象限。若点在函数的图象上，则的面积为（ ）

A. .B. .C. .D. .

Answer 1

【答案】C

【解析】

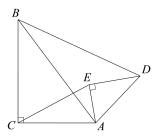
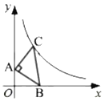
设点B的横坐标为x，过C作x轴，y轴的垂线，易证△OAB≌△DCA，可得CD=OA=1，AD=OB=x，因为点C在y=图象上，可得矩形ODCE的面积为3，列方程即可得出x的值，然后根据勾股定理求出AB的长，即可得出△ABC的面积．

解：设点B的横坐标为x，过C作CE⊥x轴于点E，CD⊥y轴于点D，

∵∠DCA+∠DAC=90°，∠DAC+∠OAB=90°，

∴∠DCA=∠OAB，

在△OAB与△DCA中，

，

∴△OAB≌△DCA（AAS），

∴CD=OA=1，AD=OB=x，

∴OD=1+x，

∵点C在y=图象上，

∴矩形ODCE的面积为3，

即1×（1+x）=3，

x=2，

∴AC=AB==，

∴S△ABC=×AB×AC=．

故选：C．