题目内容
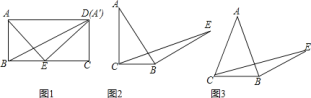
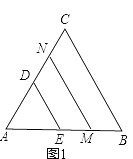
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:
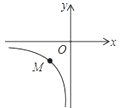
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;
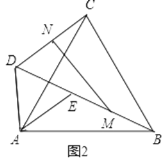
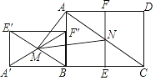
(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).
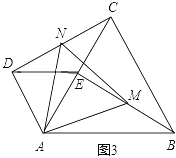
【答案】(1) CD=BE.理由见解析;(2)△AMN是等边三角形.理由见解析.
【解析】
(1)CD=BE.利用“等边三角形的三条边相等、三个内角都是60°”的性质证得△ABE≌△ACD;然后根据全等三角形的对应边相等即可求得结论CD=BE;(2)△AMN是等边三角形.首先利用全等三角形“△ABE≌△ACD”的对应角相等、已知条件“M、N分别是BE、CD的中点”、等边△ABC的性质证得△ABM≌△ACN;然后利用全等三角形的对应边相等、对应角相等求得AM=AN、∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°,所以有一个角是60°的等腰三角形的正三角形.
(1)CD=BE.理由如下:∵△ABC和△ADE为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=60°,
∵∠BAE=∠BAC﹣∠EAC=60°﹣∠EAC,
∠DAC=∠DAE﹣∠EAC=60°﹣∠EAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
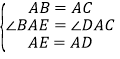 ,
,
∴△ABE≌△ACD(SAS)
∴CD=BE
(2)△AMN是等边三角形.理由如下:∵△ABE≌△ACD,
∴∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,∴BM=CN
∵AB=AC,∠ABE=∠ACD,
在△ABM和△ACN中,
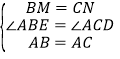 ,
,
∴△ABM≌△ACN(SAS).
∴AM=AN,∠MAB=∠NAC.
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°
∴△AMN是等边三角形