题目内容
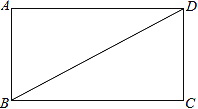
【题目】如图,在边长为10的正方形ABCD中,△PAQ是正三角形,求PB的长. 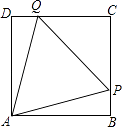
【答案】解:设PB=x, ∴PC=10﹣x,
由题意可知:AD=AB,AQ=AP
在Rt△AQD与Rt△APB中,![]()
∴Rt△AQD≌Rt△APB(HL)
∴DQ=PB=x,
∴CQ=10﹣x,
在Rt△APB中,AP2=100+x2 ,
在Rt△CQP中,AP2=CQ2+PC2 ,
∴100+x2=2(10﹣x)2
化简:x2﹣40x+100=0,
解得:x=20±10 ![]() ,
,
∵x<10,
∴PB=x=20﹣10 ![]()
【解析】设PB=x,根据正方形以及等边三角形的性质求出PQ与PC的表达式,然后利用勾股定理列出方程求出x的值.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?