ЬтФПФкШн
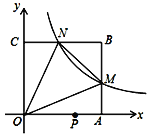
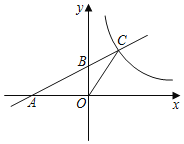
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bЃЈkЁй0ЃЉгыЗДБШР§КЏЪ§yЃН![]() ЃЈaЁй0ЃЉЕФЭМЯѓдкЕквЛЯѓЯоНЛгкAЁЂBСНЕуЃЌAЕуЕФзјБъЮЊЃЈmЃЌ4ЃЉЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌСЌНгOAЁЂOBЃЌЙ§BзїBDЁЭyжсЃЌДЙзуЮЊDЃЌНЛOAгкCЃЎШєOCЃНCAЃЌ
ЃЈaЁй0ЃЉЕФЭМЯѓдкЕквЛЯѓЯоНЛгкAЁЂBСНЕуЃЌAЕуЕФзјБъЮЊЃЈmЃЌ4ЃЉЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌСЌНгOAЁЂOBЃЌЙ§BзїBDЁЭyжсЃЌДЙзуЮЊDЃЌНЛOAгкCЃЎШєOCЃНCAЃЌ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкжБЯпBDЩЯЪЧЗёДцдквЛЕуEЃЌЪЙЕУЁїAOEЪЧжБНЧШ§НЧаЮЃЌЧѓГіЫљгаПЩФмЕФEЕузјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() ЃЌyЃНЉ
ЃЌyЃНЉ![]() x+6ЃЛЃЈ2ЃЉ
x+6ЃЛЃЈ2ЃЉ![]() ЃЎЃЈ3ЃЉEзјБъЮЊЃЈЉ
ЃЎЃЈ3ЃЉEзјБъЮЊЃЈЉ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЁОНтЮіЁП
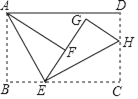
ЃЈ1ЃЉЯШРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЗДБШР§КЏЪ§НтЮіЪНЃЌНјЖјШЗЖЈГіЕуAЕФзјБъЃЌдйгУД§ЖЈЯЕЪ§ЗЈЧѓГівЛДЮКЏЪ§НтЮіЪНЃЛ
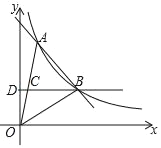
ЃЈ2ЃЉЙ§ЕуAзїAFЁЭxжсгкFНЛOBгкGЃЌЯШЧѓГіOBЕФНтЮіЪНЃЌНјЖјЧѓГіAGЃЌгУШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУГіНсТлЃЎ
ЃЈ3ЃЉЗжШ§жжЧщаЮЗжБ№ЬжТлЧѓНтМДПЩНтОіЮЪЬтЃЛ
НтЃКЃЈ1ЃЉЁпЕуBЃЈ3ЃЌ2ЃЉдкЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЃЌ
ЕФЭМЯѓЩЯЃЌ
ЁрaЃН3ЁС2ЃН6ЃЌ
ЁрЗДБШР§КЏЪ§ЕФБэДяЪНЮЊyЃН![]() ЃЌ
ЃЌ
ЁпЕуAЕФзнзјБъЮЊ4ЃЌ
ЁпЕуAдкЗДБШР§КЏЪ§yЃН![]() ЭМЯѓЩЯЃЌ
ЭМЯѓЩЯЃЌ
ЁрAЃЈ![]() ЃЌ4ЃЉЃЌ
ЃЌ4ЃЉЃЌ
Ёр ЃЌЁр
ЃЌЁр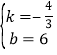 ЃЌ
ЃЌ
ЁрвЛДЮКЏЪ§ЕФБэДяЪНЮЊyЃНЉ![]() x+6ЃЛ
x+6ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуAзїAFЁЭxжсгкFНЛOBгкGЃЌ

ЁпBЃЈ3ЃЌ2ЃЉЃЌ
ЁржБЯпOBЕФНтЮіЪНЮЊyЃН![]() xЃЌ
xЃЌ
ЁрGЃЈ![]() ЃЌ1ЃЉЃЌ
ЃЌ1ЃЉЃЌ
AЃЈ![]() ЃЌ4ЃЉЃЌ
ЃЌ4ЃЉЃЌ
ЁрAGЃН4Љ1ЃН3ЃЌ
ЁрSЁїAOBЃНSЁїAOG+SЁїABGЃН![]() ЁС3ЁС3ЃН
ЁС3ЁС3ЃН![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ2жаЃЌ
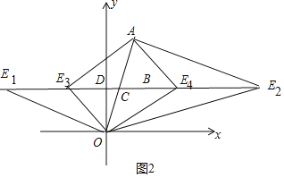
ЕБЁЯAOE1ЃН90ЁуЪБЃЌЁпжБЯпACЕФНтЮіЪНЮЊyЃН![]() xЃЌ
xЃЌ
ЁржБЯпOE1ЕФНтЮіЪНЮЊyЃНЉ![]() xЃЌ
xЃЌ
ЕБyЃН2ЪБЃЌxЃНЉ![]() ЃЌ
ЃЌ
ЁрE1ЃЈЉ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЕБЁЯOAE2ЃН90ЁуЪБЃЌ
жБЯпOE1ЦНаажБЯпOE2
ЩшжБЯпOE2ЕФНтЮіЪНЮЊyЃНЉ![]() x+bЃЌ
x+bЃЌ
ЁржБЯпЙ§ЕуAЃЈ![]() ЃЌ4ЃЉЃЌдђb=
ЃЌ4ЃЉЃЌдђb=![]()
ЁржБЯпOE2ЕФНтЮіЪНЮЊyЃНЉ![]() x+
x+![]() ЃЌ
ЃЌ
ЕБyЃН2ЪБЃЌxЃН![]() ЃЌ
ЃЌ
ЁрE2ЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ
ЕБЁЯOEAЃН90ЁуЪБЃЌ
ЁпAЃЈ![]() ЃЌ4ЃЉЃЌЁрOA=
ЃЌ4ЃЉЃЌЁрOA=![]()
ЁрACЃНOCЃНCEЃН![]() ЃЌ
ЃЌ
ЁпCЃЈ![]() ЃЌ2ЃЉЃЌ
ЃЌ2ЃЉЃЌ
ЁрПЩЕУE3ЃЈ![]() ЃЌ2ЃЉЃЌE4ЃЈ
ЃЌ2ЃЉЃЌE4ЃЈ![]() ЃЌ2ЃЉЃЌ
ЃЌ2ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуEзјБъЮЊЃЈЉ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЛђЃЈ
ЃЌ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЃЎ
ЃЌ2ЃЉЃЎ

ЁОЬтФПЁПдкдЊЕЉЦкМфЃЌФГЩЬГЁМЦЛЎЙКНјМзЁЂввСНжжЩЬЦЗЃЎ
ЃЈ1ЃЉвбжЊМзЁЂввСНжжЩЬЦЗЕФНјМлЗжБ№ЮЊ30дЊЃЌ70дЊЃЌИУЩЬГЁЙКНјМзЁЂввСНжжЩЬЦЗЙВ50МўашвЊ2300дЊЃЌдђИУЩЬГЁЙКНјМзЁЂввСНжжЩЬЦЗИїЖрЩйМўЃП
ЃЈ2ЃЉИУЩЬГЁЙВЭЖШы9500дЊзЪН№ЙКНјетСНжжЩЬЦЗШєИЩМўЃЌетСНжжЩЬЦЗЕФНјМлКЭЪлМлШчБэЫљЪОЃК
Мз | вв | |
НјМлЃЈдЊ/МўЃЉ | 30 | 70 |
ЪлМлЃЈдЊ/МўЃЉ | 50 | 100 |
ШєШЋВПЯњЪлЭъКѓПЩЛёРћ5000дЊЃЈРћШѓЃНЃЈЪлМлЉНјМлЃЉЁСЯњСПЃЉЃЌдђИУЩЬГЁЙКНјМзЁЂввСНжжЩЬЦЗИїЖрЩйМўЃП