题目内容
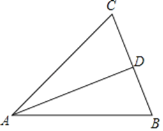
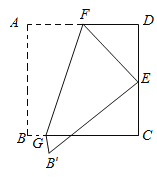
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.
【答案】2![]() .
.
【解析】
过点G作GH⊥AD于H,根据翻折变换的性质可得GF⊥AE,然后求出∠GFH=∠D,再利用“角角边”证明△ADE和△GHF全等,根据全等三角形对应边相等可得GF=AE,再利用勾股定理列式求出AE,从而得解.
如图,过点G作GH⊥AD于H,

则四边形ABGH中,HG=AB,
由翻折变换的性质得GF⊥AE,
∵∠AFG+∠DAE=90°,∠AED+∠DAE=90°,
∴∠AFG=∠AED,
∵四边形ABCD是正方形,
∴AD=AB,
∴HG=AD,
在△ADE和△GHF中,
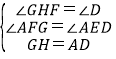 ,
,
∴△ADE≌△GHF(AAS),
∴GF=AE,
∵点E是CD的中点,
∴DE=![]() CD=2,
CD=2,
在Rt△ADE中,由勾股定理得,AE=![]() ,
,
∴GF的长为2![]() .
.
故答案为:2![]() .
.

练习册系列答案
相关题目
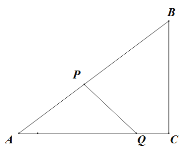
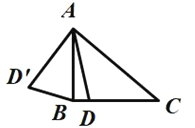
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 为
为![]() ,
,![]() 为
为![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
的变化而变化的规律进行了探究,下面是小明的探究过程.请补充完整(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 |
| 0.7 | 0.9 | 1.1 |
![]() 的值约为____________;
的值约为____________;
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像.

(3)结合画出的函数图像,解决问题:
①线段![]() 的长度的最小值约为____________
的长度的最小值约为____________![]() ;
;
②![]() ,则
,则![]() 的长度
的长度![]() 的取值范围是____________.
的取值范围是____________.