题目内容
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于任意一条对角线的平方,则称该四边形为勾股四边形.
(1)请在你学过的特殊四边形中,写出两种勾股四边形______、______;
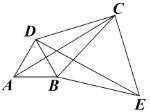
(2)如图,将钝角△ABC绕点B顺时针旋转60°得到△DBE,连接AD、DC、CE,若∠DCE=90°.求证:四边形ABCD为勾股四边形.

【答案】(1)矩形(或长方形)、正方形、直角梯形等;(2)证明见解析.
【解析】
(1)由勾股四边形的定义和特殊四边形的性质,则可得出;
(2)由旋转的性质可知△ABC≌△DBE,从而可得BC=BE,由∠CBE=60°可得△BCE为等边三角形,可得∠BCE=60°,从而可知△DCE是直角三角形,再利用勾股定理即可解决问题.
解:(1)由题意可得:矩形,正方形是勾股四边形,
故答案为:矩形,正方形;
(2)证明:∵![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]()
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() 为等边三角形
为等边三角形
∴![]()
又∵在![]() 中
中
∴![]()
∴![]()
∴![]()
∵在四边形![]() 中
中![]()
∴四边形![]() 为勾股四边形
为勾股四边形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目