题目内容
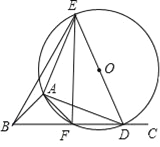
【题目】如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别在∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,点D在点F的右侧,O为圆心.
(1)求证:△ABD≌△AFE
(2)若AB=4![]() ,8
,8![]() <BE≤4
<BE≤4![]() ,求⊙O的面积S的取值范围.
,求⊙O的面积S的取值范围.
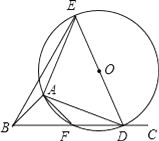
【答案】(1)证明见解析(2)16π<S≤40π
【解析】试题分析:(1)利用同弧所对的圆周角相等得出两组相等的角,再利用已知AE=AD,得出三角形全等;(2)利用△ABD≌△AFE,和已知条件得出BF的长,利用勾股定理和8![]() <BE≤4
<BE≤4![]() ,求出EF,DF的取值范围,
,求出EF,DF的取值范围, ![]() ,所以利用二次函数的性质求出最值.
,所以利用二次函数的性质求出最值.
试题解析:(1)连接EF,
∵△ADE是等腰直角三角形,AE=AD,
∴∠EAD=90°,∠AED=∠ADE=45°,
∵![]() ,
,
∴∠ADE=∠AFE=45°,
∵∠ABD=45°,
∴∠ABD=∠AFE,
∵![]() ,
,
∴∠AEF=∠ADB,
∵AE=AD,
∴△ABD≌△AFE;
(2)∵△ABD≌△AFE,
∴BD=EF,∠EAF=∠BAD,
∴∠BAF=∠EAD=90°,
∵![]() ,
,
∴BF=![]() =8,
=8,
设BD=x,则EF=x,DF=x﹣8,
∵BE2=EF2+BF2, ![]() <BE≤
<BE≤![]() ,
,
∴128<EF2+82≤208,
∴8<EF≤12,即8<x≤12,
则![]() =
=![]() ,
,
∵![]() >0,
>0,
∴抛物线的开口向上,
又∵对称轴为直线x=4,
∴当8<x≤12时,S随x的增大而增大,
∴16π<S≤40π.

练习册系列答案
相关题目