题目内容
【题目】已知4个数:(-1)2015,|-2|,-(-1.5),-3,其中正数的个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
根据有理数的乘方求出(-1)2005 和-32,根据绝对值的性质求出|-2|,根据相反数的定义求出-(-1.5) 的值即可作出判断.
∵(-1)2005 =-1,
|-2|=2,
-(-1.5)=1.5,
-32 =-9.
可见其中正数有|-2|、-(-1.5),共2个,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况: 
(1)将下面的表格补充完整:
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | … |
【题目】问题情景:
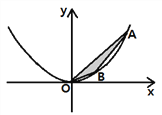
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题:
探究:当a=1时,
mn | m | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
归纳证明:
对任意m、n(m>n>0),猜想S=_________________ (用a,m,n表示),并证明你的猜想.
拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=____ (用a, m,n表示).