题目内容
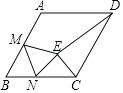
【题目】在菱形ABCD中,∠B=60°,BC=2cm,M为AB的中点,N为BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE,CE,当△CDE为等腰三角形时,线段BN的长为_____.
【答案】![]() 或2
或2
【解析】
分两种情况:①如图1,当DE=DC时,连接DM,作DG⊥BC于G,由菱形的性质得出AB=CD=BC=2,AD∥BC,AB∥CD,得出∠DCG=∠B=60°,∠A=120°,DE=AD=2,
求出DG=![]() ,CG=
,CG=![]() ,BG=BC+CG=3,由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,证明△ADM≌△EDM,得出∠A=∠DEM=120°,证出D、E、N三点共线,设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,由勾股定理得出方程,解方程即可;
,BG=BC+CG=3,由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,证明△ADM≌△EDM,得出∠A=∠DEM=120°,证出D、E、N三点共线,设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,由勾股定理得出方程,解方程即可;
②如图2,当CE=CD上,CE=CD=AD,此时点E与A重合,N与点C重合,CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(含CE=DE这种情况).
解:分两种情况,
①如图1,当DE=DC时,连接DM,作DG⊥BC于G,
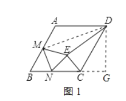
∵四边形ABCD是菱形,∴AB=CD=BC=2,AD∥BC,AB∥CD,
∴∠DCG=∠B=60°,∠A=120°,∴DE=AD=2,
∵DG⊥BC,∴∠CDG=90°-60°=30°,
∴CG=![]() CD=1,∴DG=
CD=1,∴DG=![]() CG=
CG=![]() ,BG=BC+CG=3,
,BG=BC+CG=3,
∵M为AB的中点,∴AM=BM=1,
由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,
在△ADM和△EDM中,AD=ED,AM=EM ,DM=DM,
∴△ADM≌△EDM(SSS),∴∠A=∠DEM=120°,
∴∠MEN+∠DEM=180°,∴D、E、N三点共线,
设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,
由勾股定理得:(3-x)+(![]() ) =(x+2),
) =(x+2),
解得:x=![]() ,,即BN=
,,即BN=![]() ;
;
②当CE=CD时,CE=CD=AD,此时点E与A重合,N与点C重合,如图2所示:
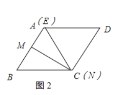
CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(符合题干要求);
综上所述,当△CDE为等腰三角形时,线段BN的长为![]() 或2;
或2;
故答案为![]() 或2.
或2.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案