题目内容
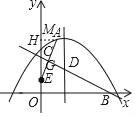
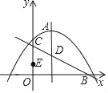
【题目】如图，二次函数y＝ax2+bx+c的图象与x轴的一个交点坐标
，顶点A的坐标为
．直线
交x轴于点B，交y轴于点C，与抛物线的对称轴交于点D，E为y轴上的一个动点．
（1）求这条抛物线的解析式和点D的坐标；
（2）若以C、D、E为顶点的三角形与△ACD相似，求点E的坐标；
（3）若点E关于直线BC的对称点M恰好落在抛物线上，求点M的坐标．
【答案】（1）这条抛物线的解析式为：y＝
，点D的坐标为：（2，2）．（2）E点坐标为（0，1）或（0，
）．（3）M点坐标为（2，
）或（﹣1，
）．
【解析】
（1）将函数解析式写成顶点式，代入顶点及抛物线与x轴交点坐标可以求得解析式；点D横坐标即为顶点横坐标，代入直线解析式即可求得点D纵坐标，从而可得结论；
（2）设点E坐标为（0，m），用含m的代数式表示出CE，利用相似三角形的性质列比例式可解；
（3）从点E关于直线BC的对称点M向y轴作垂直，由∠MEH与∠OBC相等，利用三角函数求得相关线段的长度，从而用一个未知数表示出点M的坐标，再将其代入抛物线解析式可求得这个未知数，从而得解．
（1）∵二次函数y＝ax2+bx+c的图象与x轴的一个交点坐标（2+3
，0），顶点A的坐标为（2，），
设其顶点式解析式为y＝a（x﹣2）2+，把（2+3，0）代入可得：a＝﹣
，
∴y＝﹣（x﹣2）2+，即y＝，
∵直线
与抛物线的对称轴交于点D，当x＝2时，y＝2
∴点D坐标为（2，2）．
∴这条抛物线的解析式为：y＝，点D的坐标为：（2，2）．
（2）设点E坐标为（0，m）
∵直线交x轴于点B，交y轴于点C，当x＝0时，y＝3；当y＝0时，x＝6，
∴点C坐标为（0，3），点B坐标为（6，0），
∴CD＝
，AD＝
，CE＝3﹣m，
①当△ADC∽△DCE时，
，即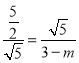
，解得m＝1；
②当△ADC∽△ECD时，
，即
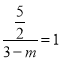，解得m＝，
∴E点坐标为（0，1）或（0，）．
（3）如图，作MH⊥y轴于点H，设ME与BC交于点G，MH＝m，则∠MEH＝∠OBC
∴tan∠OBC＝tan∠MEH＝，
∴HE＝2m，EM＝m
在Rt△CEG中，EG＝EM＝
，
∴CG＝
m ，CE＝
m ，
∴OE＝OC﹣CE＝3﹣m ，
∴OH＝OE+EH＝3﹣m+2m＝3+
m，
∴点M坐标为（m，3+m），
把M（m，3+m）代入y＝﹣（x﹣2）2+得：m1＝2，m2＝﹣1，
∴M点坐标为（2，）或（﹣1，
）．
