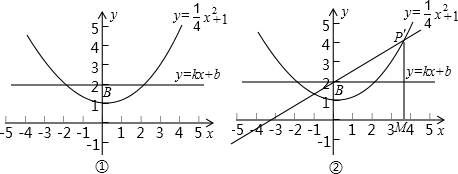��Ŀ����
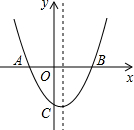
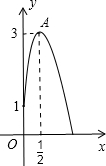
��֪������y=��3-m��x2+2��m-3��x+4m-m2����͵�A����������3��ֱ��y=mx+b������A����y�ύ�ڵ�B����x�ύ�ڵ�C��
��1������������ֱ��AB�Ľ���ʽ��
��2����ֱ��AB�Ƶ�O˳ʱ����ת90�㣬��x�ύ�ڵ�D����y�ύ�ڵ�E����sin��BDE��ֵ��
��3����B����x���ƽ����BG����M��ֱ��BG�ϣ��ҵ������ߵĶԳ���ľ���Ϊ6�����N��ֱ��BG�ϣ�����ֱ��д��ʹ�á�AMB+��ANB=45��ĵ�N�����꣮

��1������������ֱ��AB�Ľ���ʽ��
��2����ֱ��AB�Ƶ�O˳ʱ����ת90�㣬��x�ύ�ڵ�D����y�ύ�ڵ�E����sin��BDE��ֵ��
��3����B����x���ƽ����BG����M��ֱ��BG�ϣ��ҵ������ߵĶԳ���ľ���Ϊ6�����N��ֱ��BG�ϣ�����ֱ��д��ʹ�á�AMB+��ANB=45��ĵ�N�����꣮

��1����y=��3-m��x2+2��m-3��x+4m-m2�ģ�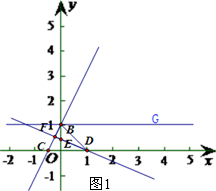
�������ߵĶԳ���x=-
=-
=1��
��������y=��3-m��x2+2��m-3��x+4m-m2����͵�A����������3
�������ߵĶ���ΪA��1��3��
��m2-5m+6=0��
��m=3��m=2��
��3-m��0��
��m��3
��m=2��
�������ߵĽ���ʽΪ��y=x2-2x+4��
ֱ��Ϊy=2x+b��
��ֱ��y=mx+b������A��1��3��
��3=2+b��
��b=1��
��ֱ��ABΪ��y=2x+1��
��2����x=0����y=1������y=0����x=-
��
��B��0��1����C��-
��0��
��ֱ��AB��O��˳ʱ����ת900����DE��BC���ڵ�F
��D��1��0����E��0��
������CFD=90�㣬
��OB=OD=1OC=
����CD=
��Rt��BOC�У��ɹ��ɶ�������CB=
��BD=
��
��CD•OB=CB•DF��
��DF=
��
���ɹ��ɶ�������BF=
��
��Sin��BDE=
=
=
��
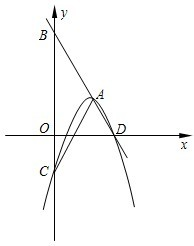
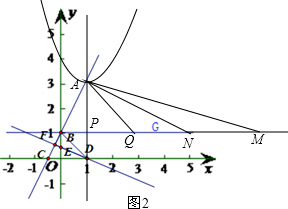
��3����ͼ2����BG��ȡһ��Q��ʹAP=QP��
���AQP=45�㣮
���ANB+��QAN=��QAM+��AMB=45�㣮
�ߡ�AMB+��ANB=45�㣬
���ANB=��QAM��
���AQN����MQA��
��
=
��
��AD=3��OD=1��
��AP=QP=2��
��QM=4��AQ=2
��
��MP=6��
��MQ=4��
��
=
��
��QN=2��
��BN=5��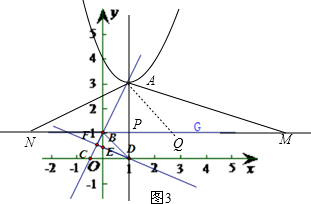
��N��5��1����
��ͼ3����BG��ȡһ��Q��ʹAP=QP��
���AQP=45�㣮
���ANB+��AMB=��QAM+��AMB=45�㣮
���ANB=��QAM��
���AQM����NAM��
��
=
��
��AD=3��OD=1��
��AP=QP=2��
��QM=4��BM=7��AQ=2
��
��MP=6��
��MQ=4��AM=2
��
��
=
��
��MN=10��
��BN=3��
��N��-3��1����
��N��-3��1����5��1����

�������ߵĶԳ���x=-
| b |
| 2a |
| 2(m-3) |
| 2(3-m) |
��������y=��3-m��x2+2��m-3��x+4m-m2����͵�A����������3
�������ߵĶ���ΪA��1��3��
��m2-5m+6=0��
��m=3��m=2��
��3-m��0��
��m��3
��m=2��
�������ߵĽ���ʽΪ��y=x2-2x+4��
ֱ��Ϊy=2x+b��
��ֱ��y=mx+b������A��1��3��
��3=2+b��
��b=1��
��ֱ��ABΪ��y=2x+1��
��2����x=0����y=1������y=0����x=-
| 1 |
| 2 |
��B��0��1����C��-
| 1 |
| 2 |
��ֱ��AB��O��˳ʱ����ת900����DE��BC���ڵ�F
��D��1��0����E��0��
| 1 |
| 2 |
��OB=OD=1OC=
| 1 |
| 2 |
| 3 |
| 2 |
��Rt��BOC�У��ɹ��ɶ�������CB=
| ||
| 2 |
| 2 |
��CD•OB=CB•DF��
��DF=
| 3 |
| 5 |
| 5 |
���ɹ��ɶ�������BF=
| ||
| 5 |

��Sin��BDE=
| BF |
| BD |
| ||||
|
| ||
| 10 |
��3����ͼ2����BG��ȡһ��Q��ʹAP=QP��
���AQP=45�㣮
���ANB+��QAN=��QAM+��AMB=45�㣮
�ߡ�AMB+��ANB=45�㣬
���ANB=��QAM��
���AQN����MQA��
��
| AQ |
| MQ |
| QN |
| QA |
��AD=3��OD=1��
��AP=QP=2��
��QM=4��AQ=2
| 2 |
��MP=6��
��MQ=4��
��
2
| ||
| 4 |
| QN | ||
2
|
��QN=2��
��BN=5��

��N��5��1����
��ͼ3����BG��ȡһ��Q��ʹAP=QP��
���AQP=45�㣮
���ANB+��AMB=��QAM+��AMB=45�㣮
���ANB=��QAM��
���AQM����NAM��
��
| AM |
| MN |
| QM |
| AM |
��AD=3��OD=1��
��AP=QP=2��
��QM=4��BM=7��AQ=2
| 2 |
��MP=6��
��MQ=4��AM=2
| 10 |
��
2
| ||
| MN |
| 4 | ||
2
|
��MN=10��
��BN=3��
��N��-3��1����
��N��-3��1����5��1����

��ϰ��ϵ�д�
 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
�����Ŀ