题目内容
【题目】已知Rt△ABC,AB=AC,点D在△ABC的外部,且∠DAC<90°,
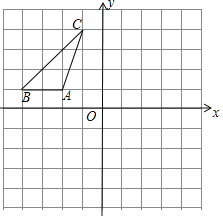
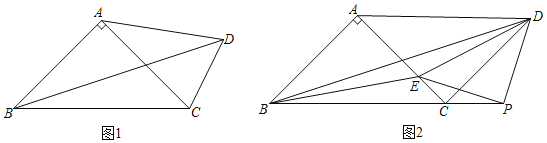
(1)如图1,若AD=AC,求∠BDC;
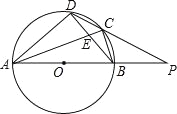
(2)如图2,点E在线段AC上,线段DE的垂直平分线交BC的延长线于点P.当点D正好和点B关于线段AC的中点对称时,
①证明:△PDE为直角三角形;
②连接BE、AD,若![]() ,直接写出
,直接写出![]() =_____.
=_____.
【答案】(1)∠BDC=45°;(2)①证明见解析;②8.
【解析】
(1)设∠DAC=x,则∠BAD=90°+x,由等腰三角形的性质可得∠ADB=45°﹣![]() ,∠ADC=90°﹣
,∠ADC=90°﹣![]() ,即可求解;
,即可求解;
(2)①如图2,过点P作PH⊥CD,PG⊥AC,由中心对称的性质可得AO=CO,BO=DO,可证△AOB≌△COD,可得AB=CD,∠BAC=∠ACD=90°,由“AAS”可证△PHC≌△PGC,可得PH=PG,由“HL”可证Rt△PEG≌Rt△PDH,可得∠EPG=∠HPD,即可得结论;
②设BC=8a,BP=11a,则CP=3a,由等腰直角三角形的性质可求AB=AC=CD=4![]() a,CH=HP=CG=GP=
a,CH=HP=CG=GP=![]() a,可求AE,EC的长,由三角形的面积公式可求解.
a,可求AE,EC的长,由三角形的面积公式可求解.
解:(1)设∠DAC=x,则∠BAD=90°+x,
∵AD=AC=AB,
∴∠ADB=45°﹣![]() ,∠ADC=90°﹣
,∠ADC=90°﹣![]() ,
,
∴∠BDC=∠ADC﹣∠ADB=45°;
(2)如图2,过点P作PH⊥CD,PG⊥AC

∵线段DE的垂直平分线交BC的延长线于点P.
∴EP=DP,
∵点D正好和点B关于线段AC的中点O对称,
∴AO=CO,BO=DO,且∠AOB=∠COD,
∴△AOB≌△COD(SAS)
∴AB=CD,∠BAC=∠ACD=90°,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,且∠ACD=90°,
∴∠PCG=∠PCH=45°,且PC=PC,∠PGC=∠PHC=90°,
∴△PHC≌△PGC(AAS)
∴PH=PG,且EP=DP,
∴Rt△PEG≌Rt△PDH(HL),
∴∠EPG=∠HPD,
∵∠HCG=∠HCP+∠GCP=90°,PH⊥CD,PG⊥AC,
∴∠HPG=90°,
∴∠EPG+∠EPH=90°,
∴∠DPH+∠EPH=90°,即∠DPE=90°
∴△PDE为直角三角形;
②如图2,

∵![]() ,
,
∴设BC=8a,BP=11a,则CP=3a,
∵AB=AC,∠BAC=90°,BC=8a,
∴AB=AC=4![]() a,
a,
∴CD=4![]() a,
a,
∵∠PCH=∠PCG=45°,PH⊥CD,PG⊥AC,
∴∠PCH=∠PCG=∠HPC=∠GCP=45°,
∴CH=HP,CG=GP,且CP=3a,PH⊥CD,PG⊥AC,
∴CH=HP=CG=GP=![]() a,
a,
∴DH=CD﹣CH=![]() a,
a,
∵Rt△PEG≌Rt△PDH,
∴EG=DH=![]() a,
a,
∴EC=EG﹣CG=![]() a,
a,
∴AE=![]() a,
a,
∴![]() =
=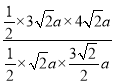 =8,
=8,
故答案为8.