题目内容
【题目】某学习小组在研究函数y= 
x3﹣2x的图象与性质时，已列表、描点并画出了图象的一部分．
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
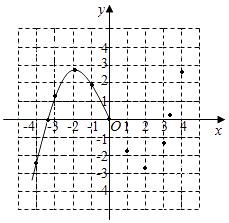
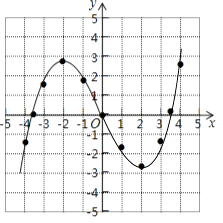
（1）请补全函数图象；
（2）方程 x3﹣2x=﹣2实数根的个数为；
（3）观察图象，写出该函数的两条性质．
【答案】
（1）解：补全函数图象如图所示，
（2）3
（3）解：由图象知，
①此函数在实数范围内既没有最大值，也没有最小值，
②此函数在x＜﹣2和x＞2，y随x的增大而增大，
③此函数图象过原点，
④此函数图象关于原点对称．
【解析】
（ 2 ）如图1，
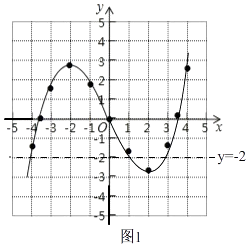
作出直线y=﹣2的图象，
由图象知，函数y= 
x3﹣2x的图象和直线y=﹣2有三个交点，
∴方程 x3﹣2x=﹣2实数根的个数为3，
所以答案是：3.
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
练习册系列答案
天天练口算系列答案
相关题目
【题目】观察下面三行数：
第1列 | 第2列 | 第3列 | 第4列 | … | 第n列 |
﹣3 | 9 | a | 81 | … | r |
1 | ﹣3 | 9 | b | … | s |
﹣2 | 10 | c | 82 | … | t |
（1）直接写出a，b，c的值；
（2）直接写出r，s，t的值；
（3）设x，y，z分别为第①②③行的第2019个数，求x+6y+z的值．
