题目内容
【题目】如图,将两块直角三角板的直角顶点C叠放在一起.
(1)若∠DCE=28°10',求∠ACB的度数;
(2)若∠ACB=148°21',求∠DCE的度数;
(3)直接写出∠ACB与∠DCE的数量关系.
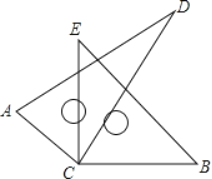
【答案】(1)151°50'; (2)31°39'; (3)∠ACB+∠DCE=180°.
【解析】
(1)根据角的和差关系可直接得到∠ACB=90°+90°-28°10'=151°50';
(2)首先计算出∠ACE的度数,然后再根据∠ACD=90°可得∠ECD的度数;
(3)把∠ACB+∠ECD化为∠ECB+∠ACE+∠ECD,再根据∠ACD=∠ECB=90°可得∠ACB+∠DCE=180°.
(1)∵∠DCB=28°10',∠ACD=90°,
∴∠ACB=90°+90°﹣28°10'=151°50';
(2)∵∠ACB=148°21',∠ECB=90°,
∴∠ACE=148°21'﹣90°=58°21',
∵∠ACD=90°,
∴∠ECD=31°39';
(3)∠ACB+∠DCE=180°,
∵∠ACD=∠ECB=90°.
∴∠ACB+∠ECD=∠ECB+∠ACE+∠ECD=90°+90°=180°.

练习册系列答案
相关题目