题目内容
【题目】如图,已知D是△ABC中一边BC上的中点 ,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
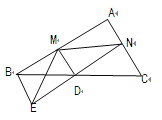
(1)求证:BE=CN
(2)试判断BM+CN与MN的大小关系,并说明理由.
【答案】(1)证明见解析;(2)BM+CN>MN.
【解析】
试题分析:(1)根据平行线的性质可证∠C=∠DBE,根据中点的定义可证BD=CD,根据AAS可证△BDE≌△CDN,根据全等三角形的性质可证DE=DN,BE=CN;
(2)根据DM⊥EN,可得∠MDE=∠MDN=90°,因为DE=DN,根据中垂线的性质可证ME=MN,根据三角形三边的关系可证BM+BE>ME,所以可证
试题解析:(1)∵AC//BE,BM+CN>MN.
∴∠C=∠DBE,
∵D是BC中点,
∴BD=CD,
又∠BDE=∠CDN,
∴△BDE≌△CDN(AAS),
∴DE=DN,BE=CN,
(2)∵DM⊥EN,
∴∠MDE=∠MDN=90°,
∵DE=DN,
∴ME=MN,
在△BME中BM+BE>ME,
又BE=CN,ME=MN,
∴BM+CN>MN.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目