Question

【题目】在平面直角坐标系中，边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图）．在旋转正方形OABC的过程中，△MBN的周长为 ．

Answer 1

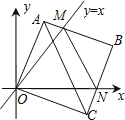
【答案】6.

【解析】

试题解析：∵A点第一次落在直线y=x上时停止旋转，直线y=x与y轴的夹角是45°，

∴OA旋转了45°．

如图所示：延长BA交y轴于E点，

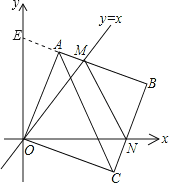
则∠AOE=45°-∠AOM，∠CON=90°-45°-∠AOM=45°-∠AOM，

∴∠AOE=∠CON．

又∵OA=OC，∠OAE=180°-90°=90°=∠OCN，

在△OAE和△OCN中，

，

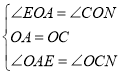∴△OAE≌△OCN（ASA）．

∴OE=ON，AE=CN．

在△OME和△OMN中，

，

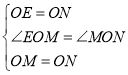∴△OME≌△OMN（SAS）．

∴MN=ME=AM+AE．

∴MN=AM+CN，

∴△MBN的周长为：MN+BN+BM=AM+CN+BN+BM=AB+BC=6．