题目内容
已知关于 的一元二次方程
的一元二次方程 .
.
(1)若 是这个方程的一个根,求
是这个方程的一个根,求 的值和它的另一根;
的值和它的另一根;
(2)对于任意的实数 ,判断原方程根的情况,并说明理由.
,判断原方程根的情况,并说明理由.
 的一元二次方程
的一元二次方程 .
.(1)若
 是这个方程的一个根,求
是这个方程的一个根,求 的值和它的另一根;
的值和它的另一根;(2)对于任意的实数
 ,判断原方程根的情况,并说明理由.
,判断原方程根的情况,并说明理由.(1)1,2;(2)原方程总有两个实数根,理由见解析.
试题分析:(1)把x=1代入方程得到关于k的方程,求出k的值,再把k的值代入原方程,然后利用因式分解法解方程求出方程的另一根;
(2)计算判别式得到△=(k+2)2-4×2k=k2-4k+4=(k-2)2,根据非负数的性质得到△≥0,然后根据判别式的意义判断方程根的情况.
试题解析:(1)∵
 是方程
是方程 的一个根,
的一个根,∴
 ,
,解得
 ,
,∴原方程为
 ,
,解得
 ,
, ,
,∴原方程的另一根为

(2)对于任意的实数
 ,原方程总有两个实数根,
,原方程总有两个实数根,∵



∴对于任意的实数k,原方程总有两个实数根.
考点: 1.根的判别式;2.解一元二次方程-因式分解法.

练习册系列答案
相关题目
 x﹣4=0.
x﹣4=0. ,则此三角形的周长为 .
,则此三角形的周长为 .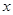 的一元二次方程
的一元二次方程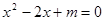 有两个不相等的实数根,则
有两个不相等的实数根,则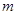 的取值范围是( )。
的取值范围是( )。



 有一个根为2,则另一根为( )
有一个根为2,则另一根为( ) 且
且 ,则关于
,则关于 的一元二次方程
的一元二次方程 必有一个定根,它是_______.
必有一个定根,它是_______.