题目内容
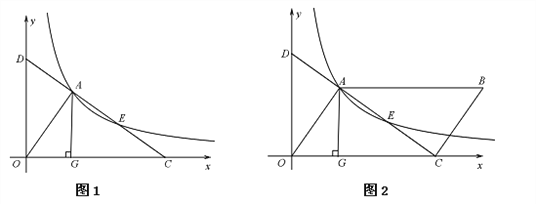
【题目】如图1,直线![]() 交x轴于点C,交y轴于点D,与反比例函数
交x轴于点C,交y轴于点D,与反比例函数![]() 的图像交于两点A、E,AG⊥x轴,垂足为点G,S△AOG=3.
的图像交于两点A、E,AG⊥x轴,垂足为点G,S△AOG=3.
(1)k = ;
(2)求证:AD =CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积
【答案】(1)k=6;
(2)证明见解析;
(3)S平行四边形OABC=18
【解析】(1)设A(m,n),由题意 ![]() OGAG=3,推出mn=6,由点A在y=
OGAG=3,推出mn=6,由点A在y=![]() 上,推出k=mn=6.
上,推出k=mn=6.
(2)如图1中,作AN⊥OD于N,EM⊥OC于M.设直线CD的解析式为y=k′x+b,A(x1,y1),E(x2,y2).首先证明EM=﹣k′AN,EM=﹣k′MC,推出AN=CM,再证明△DAN≌△ECM,即可解决问题.
(3)如图2中,连接GD,GE.由EA=EC,AD=EC,推出AD=AE=EC,推出S△ADG=S△AGE=S△GEC=3,求出△AOC的面积即可解决问题.
试题解析:
(1)解:设A(m,n),
∵![]() OGAG=3,
OGAG=3,
∴![]() mn=3,
mn=3,
∴mn=6,
∵点A在y=![]() 上,
上,
∴k=mn=6.
(2)证明:如图1中,作AN⊥OD于N,EM⊥OC于M.设直线CD的解析式为y=k′x+b,A(x1,y1),E(x2,y2).
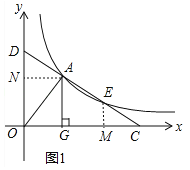
则有y1=k′x1+b,y2=k′x2+b,
∴y2﹣y1=k′(x2﹣x1),
∴![]() ﹣
﹣![]() =k′(x2﹣x1),
=k′(x2﹣x1),
∴﹣k′x1x2=6,
∴﹣k′x1=![]() ,
,
∴y2=﹣k′x1,
∴EM=﹣k′AN,
∵D(0,b),C(﹣![]() ,0),
,0),
∴tan∠DCO=![]() =﹣k′=
=﹣k′=![]() ,
,
∴EM=﹣k′MC,
∴AN=CM,
∵AN∥CM,
∴∠DAN=∠ECM,
在△DAN和△ECM中,
 ,
,
∴△DAN≌△ECM,
∴AD=EC.
(3)解:如图2中,连接GD,GE.
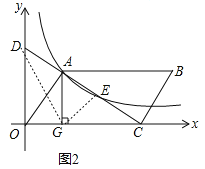
∵EA=EC,AD=EC,
∴AD=AE=EC,
∴S△ADG=S△AGE=S△GEC=3,
∵S△AOG=S△ADG=3,
∴S△AOC=3+3+3=9,
∴平行四边形ABCD的面积=2S△AOC=18.