题目内容
【题目】如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.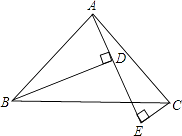
【答案】证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,
∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.
∴∠ABD=∠DAC.
∵在△ABD和△CAE中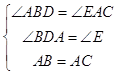 ,
,
∴△ABD≌△CAE(AAS).
∴BD=AE,EC=AD.
∵AE=AD+DE,
∴BD=EC+ED.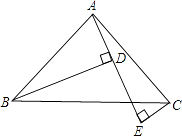
【解析】由题中AB=AC,以及AB和AC所在三角形为直角三角形,可以判断出应证明△ABD≌△CAE.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.

练习册系列答案
相关题目