题目内容
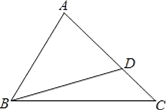
【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
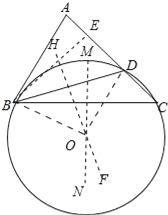
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求![]() 的值.
的值.
【答案】(1)作图见解析;(2)∠A=75°;(3)![]() =2.
=2.
【解析】试题分析:(1)利用三角形外接圆的圆心是各边垂直平分线的交点即可画出图形.
(2)只要证明△BOD是等腰直角三角形即可推出∠ABD=∠DBO=45°,利用三角形内角和定理即可解决问题.
(3)过点B作BE⊥AC,垂足为点E,设DE=x,则BD=2x,BE=![]() =
=![]() x,用x的代数式表示AD、DC即可解决问题.
x,用x的代数式表示AD、DC即可解决问题.
试题解析:(1)作BC的垂直平分线MN,作BD的垂直平分线HF,MN与FH的交点为O,以点O为圆心OB为作⊙O即可.如图所示:
;
(2)连结OB、OD,
由切线性质,知∠ABO=90°.
∵∠ACB=45°,∴∠BOD=90°(同弧所对的圆周角等于它所对的圆心角的一半).
∵OB=OD,∴∠OBD=∠ODB=45°,
由∠ABO=90°,得∠ABD=45°,∴∠A=180°﹣∠ABD﹣∠ADB=180°﹣45°﹣60°=75°;
(3)过点B作BE⊥AC,垂足为点E,
在Rt△BCE中,∵∠ACB=45°,∴∠EBC=45°,∴BE=CE.
在Rt△BDE中,∵∠DBE=90°﹣∠EDB=30°,∴BD=2DE,
设DE=x,则BD=2x,BE=![]() =
=![]() xDC=CE﹣DE=BE﹣DE=(
xDC=CE﹣DE=BE﹣DE=(![]() ﹣1)x.
﹣1)x.
AE=AD﹣DE=AD﹣x.
在△ABC和△ADB中,∵∠ABD=∠ACB=45°,∠A为公共角,∴△ABC∽△ADB,
∴![]() ,即AB2=ACAD,即
,即AB2=ACAD,即
AB2=(AD+DC)AD=AD2+AD(![]() ﹣1)x ①.
﹣1)x ①.
在Rt△ABE中,由勾股定理,得AB2=AE2+BE2=(AD﹣x)2+(![]() x)2 ②.
x)2 ②.
由①、②,得AD2+AD(![]() ﹣1)x=(AD﹣x)2+(
﹣1)x=(AD﹣x)2+(![]() x)2,
x)2,
化简整理,解得AD=2(![]() ﹣1)x.
﹣1)x.
∴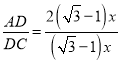 =2,
=2,
∴![]() =2.
=2.

 名校课堂系列答案
名校课堂系列答案