题目内容
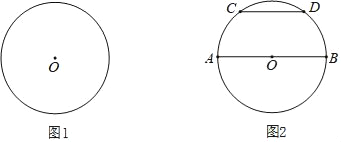
【题目】如图点O是等边![]() 内一点,
内一点,![]() ,∠ACD=∠BCO,OC=CD,
,∠ACD=∠BCO,OC=CD,
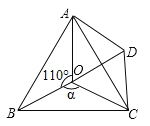
(1)试说明:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)当![]() 为多少度时,
为多少度时,![]() 是等腰三角形
是等腰三角形
【答案】(1)见解析;(2)△AOD是直角三角形,理由见解析;(3) 110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;
(2)先求得∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠CDO=60°,于是可计算出∠ADO=90°,由此可判断△AOD是直角三角形;
(3)先利用α表示出∠ADO=α-60°,∠AOD=190°-α,再进行分类讨论:当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°;当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°;当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,然后分别解方程求出对应的α的值即可.
(1)∵∠ACD=∠BCO
∴∠ACD+∠ACO=∠BCO+∠ACO=60°
又∵CO=CD
∴△COD是等边三角形;
(2)∵△COD是等边三角形
∴CO=CD
又∵∠ACD=∠BCO,AC=BC
∴△ACD≌△BCO(SAS)
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α60°,∠AOD=360°60°110°α=190°α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°α=α60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°α)+α60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°α+2(α60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.

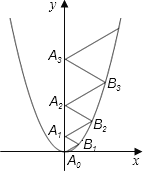
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -1 | 3 | 5 | 3 |
给出了结论:
(1)二次函数![]() 有最大值,最大值为5;(2)
有最大值,最大值为5;(2)![]() ;(3)
;(3)![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;(4)3是方程
值的增大而减小;(4)3是方程![]() 的一个根;(5)当
的一个根;(5)当![]() 时,
时,![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )
A.4B.3C.2D.1
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).