题目内容
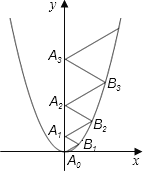
【题目】二次函数![]() 的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2008在y轴的正半轴上,点B1,B2,B3,…,B2008在二次函数
的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2008在y轴的正半轴上,点B1,B2,B3,…,B2008在二次函数![]() 位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=__.
位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=__.
【答案】2008
【解析】作B1A⊥y轴于A,B2B⊥y轴于B,B3C⊥y轴于C.
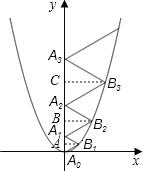
设等边△A0B1A1,△A1B2A2,△A2B3A3中,AA1=a,BA2=b,CA2=c.
①等边△A0B1A1中,A0A=a,
所以B1A=atan60°=![]() a,代入解析式得
a,代入解析式得![]() ×(
×(![]() a)2=a,
a)2=a,
解得a=0(舍去)或a=![]() ,于是等边△A0B1A1的边长为
,于是等边△A0B1A1的边长为![]() ×2=1;
×2=1;
②等边△A1B2A2中,A1B=b,
所以BB2=btan60°=![]() b,B2点坐标为(
b,B2点坐标为(![]() b,1+b)
b,1+b)
代入解析式得![]() ×(
×(![]() b)2=1+b,
b)2=1+b,
解得b=![]() (舍去)或b=1,
(舍去)或b=1,
于是等边△A1B2A2的边长为1×2=2;
③等边△A2B3A3中,A2C=c,
所以CB3=btan60°=![]() c,B3点坐标为(
c,B3点坐标为(![]() c,3+c)代入解析式得
c,3+c)代入解析式得![]() ×(
×(![]() c)2=3+c,
c)2=3+c,
解得c=1(舍去)或c=![]() ,
,
于是等边△A2B3A3的边长为![]() ×2=3.
×2=3.
于是△A2007B2008A2008的边长为2008.
故答案为:2008.

 阅读快车系列答案
阅读快车系列答案【题目】小明家承包了40亩大棚蔬菜,分别种植甲、乙两种蔬菜,有关成本,销售额如下表:
每亩成本 | 每亩销售额 | |
甲 |
| 4 |
乙 | 3 |
|
![]() 年,小明家种植甲蔬菜30亩,乙蔬菜10亩,求小明家这一年收益多少万元?
年,小明家种植甲蔬菜30亩,乙蔬菜10亩,求小明家这一年收益多少万元?
![]() 年,小明家继续用这40亩全部种植甲乙两种蔬菜,计划投入成本不少于141万元,若每亩种植成本、销售额和2015年一样,要获得最大收益,他家应该种植甲乙两种蔬菜各多少亩?
年,小明家继续用这40亩全部种植甲乙两种蔬菜,计划投入成本不少于141万元,若每亩种植成本、销售额和2015年一样,要获得最大收益,他家应该种植甲乙两种蔬菜各多少亩?
![]() 已知甲种蔬菜每亩需要有机肥600千克,乙种蔬菜每亩需要有机肥800千克
已知甲种蔬菜每亩需要有机肥600千克,乙种蔬菜每亩需要有机肥800千克![]() 根据
根据![]() 中的种植亩数,为节约运输成本,实际使用的运输每次装载的总量是计划的每次装载的总量的4倍,结果运输种植所需全部有机肥比原计划减少3次,求小明家原定的运输车辆每次可装载有机肥多少千克?
中的种植亩数,为节约运输成本,实际使用的运输每次装载的总量是计划的每次装载的总量的4倍,结果运输种植所需全部有机肥比原计划减少3次,求小明家原定的运输车辆每次可装载有机肥多少千克?