Question

【题目】对于平面直角坐标系中的点和半径为1的，定义如下：

①点的“派生点”为；

②若上存在两个点，使得，则称点为的“伴侣点”．

应用：已知点

（1）点的派生点坐标为________；在点中，的“伴侣点”是________；

（2）过点作直线交轴正半轴于点，使，若直线上的点是的“伴侣点”，求的取值范围；

（3）点的派生点在直线，求点与上任意一点距离的最小值．

Answer 1

【答案】（1）（1,0），E、D、；（2）；（3）

【解析】

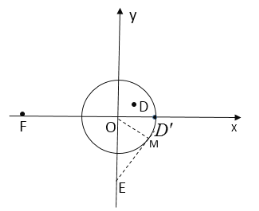
（1）根据定义即可得到点的坐标，过点E作的切线EM，连接OM，利用三角函数求出∠MEO=30°，即可得到点E是的“伴侣点”；根据点F、D、的坐标得到线段长度与线段OE比较即可判定是否是的“伴侣点”；

（2）根据题意求出，∠OGF=60°，由点是的“伴侣点”，过点P作的切线PA、PB，连接OP，OB，证明△OPG是等边三角形，得到点P应在线段PG上，过点P作PH⊥x轴于H，求出点P的横坐标是-，由此即可得到点P的横坐标m的取值范围；

（3）设点(x，-2x+6)，P（m，n），根据派生点的定义得到3m+n=6，由此得到点P在直线y=-3x+6上，设直线y=-3x+6与x轴交于点A，与y轴交于点B，过点O作OH⊥AB于H，交于点C，求出AB的长，再根据面积公式求出OH即可得到答案.

（1）∵，

∴点的派生点坐标为（1,0），

∵E(0，-2)，

∴OE=2，

过点E作的切线EM，连接OM，

∵OM=1，OE=2，∠OME=90°，

∴sin∠MEO=,

∴∠MEO=30°，

而在的左侧也有一个切点，使得组成的角等于30°，

∴点E是的“伴侣点”；

∵，

∴OF=>OE，

∴点F不可能是的“伴侣点”；

∵，（1,0），，，

∴点D、是的“伴侣点”，

∴的“伴侣点”有：E、D、，

故答案为：（1,0），E、D、；

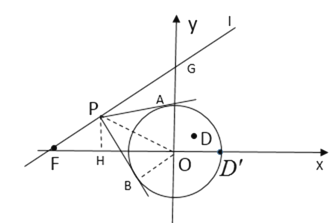
（2）如图，直线l交y轴于点G，

∵，

∴，∠OGF=60°

∵直线上的点是的“伴侣点”，

∴过点P作的切线PA、PB，且∠APB=60°，

连接OP，OB，

∴∠BOP=30°，

∵∠OBP=90°，OB=1，

∴OP=2=OG，

∴△OPG是等边三角形，

∴若点P是的“伴侣点”，则点P应在线段PG上，

过点P作PH⊥x轴于H，

∵∠POH=90°-60°=30°，OP=2，

∴PH=1，

∴OH=，即点P的横坐标是-，

∴当直线上的点是的“伴侣点”时的取值范围是；

（3）设点(x，-2x+6)，P（m，n），

根据题意得：m+n=x，m-n=-2x+6，

∴3m+n=6，

即n=-3m+6，

∴点P坐标为（m，-3m+6），

∴点P在直线y=-3x+6上，

设直线y=-3x+6与x轴交于点A，与y轴交于点B，过点O作OH⊥AB于H，交于点C，如图，则A（2,0），B（0,6），

∴,

∴,

∴,

∴,

即点P与上任意一点距离的最小值为.